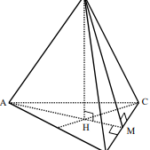
Cho hình chóp \(S.ABC\)có đáy là tam giác cân tại \(A,AB = AC = a,\widehat {BAC} = 120^\circ \), \(SA\)vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng đáy bằng \(60^\circ \). Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng A. \(\frac{{19\pi {a^3}\sqrt {19} }}{{48}}\). B. \(\frac{{19\pi {a^3}\sqrt {19} }}{{24}}\). C. … [Đọc thêm...] vềCho hình chóp \(S.ABC\)có đáy là tam giác cân tại \(A,AB = AC = a,\widehat {BAC} = 120^\circ \), \(SA\)vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng đáy bằng \(60^\circ \). Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng
Cho hình chóp \(S.ABC\)có đáy là tam giác cân tại \(A,AB = AC = a,\widehat {BAC} = 120^\circ \), \(SA\)vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng đáy bằng \(60^\circ \). Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng
Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện
