GIẢI CHI TIẾT Giải SBT Bài 3 Chương 4 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 22 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {AB} \) là hình gì?
A. Đường thẳng AB
B. Tia AB
C. Tia đối của tia AB trừ điểm A
D. Đoạn thẳng AB
Phương pháp giải
Tìm điều kiện để 2 vectơ \(\overrightarrow {AM} \), \(\overrightarrow {AB} \) ngược hướng rồi tìm vị trí điểm M
Lời giải chi tiết
Do \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng nên giá của hai vectơ này trùng nhau và B, M nằm về 2 phía của điểm A
Vậy tập hợp các điểm M thỏa mãn là tia đối của tia AB trừ điểm A
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 23 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn \(\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {AB} } \right|\) là hình gì?
A. Đường trung trực của đoạn thẳng AB
B. Đường tròn tâm A bán kính AB
C. Đường tròn tâm B bán kính AB
D. Đoạn thẳng AB
Phương pháp giải
Tìm điều kiện để độ dài 2 vectơ \(\overrightarrow {AM} \), \(\overrightarrow {AB} \) bằng nhau rồi tìm vị trí điểm M
Lời giải chi tiết
Ta có: \(\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {AB} } \right| \Leftrightarrow AM = AB\).
Vậy tập hợp các điểm M thỏa mãn \(\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {AB} } \right|\) là đường tròn tâm A bán kính AB
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 24 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
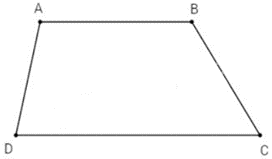
Cho hình thang ABCD có AB và CD song song với nhau. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {CD} \)
B. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
C. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
D. \(\overrightarrow {AB} = \overrightarrow {DC} \)
Phương pháp giải
Dựa vào hình vẽ xác định chiều các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {CD} \), \(\overrightarrow {DC} \) rồi kết luận
Lời giải chi tiết

Hình thang ABCD có AB // CD \( \Rightarrow \overrightarrow {AB} ,\overrightarrow {DC} \) cùng hướng
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 25 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Cho \(\overrightarrow a = \overrightarrow b \). Phát biểu nào sau đây là sai?
A. \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
B. \(\overrightarrow a \) và \(\overrightarrow b \) cùng độ dài
C. \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương
D. \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Phương pháp giải
Dựa vào định nghĩa hai vectơ bằng nhau để tìm câu sai
Lời giải chi tiết
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng nhau nếu chúng có cùng hướng và cùng độ dài \( \Rightarrow \)\(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 26 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {IA} = \overrightarrow {IB} \)
B. \(\overrightarrow {IA} \) và \(\overrightarrow {IB} \) cùng hướng
C. \(\overrightarrow {AI} = \overrightarrow {BI} \)
D. \(\overrightarrow {AI} = \overrightarrow {IB} \)
Phương pháp giải
Dựa vào định nghĩa hai vectơ bằng nhau để tìm câu đúng
Lời giải chi tiết
![]()
Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {AI} = \overrightarrow {IB} \)
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 27 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Cho 5 điểm phân biệt \(A,B,C,D,E\).
a) Viết các vectơ khác \(\overrightarrow 0 \) có cùng điểm đầu là A, điểm cuối là một trong các điểm đã cho
b) Viết các vectơ khác \(\overrightarrow 0 \) có cùng điểm cuối là B, điểm đầu là một trong các điểm đã cho
Phương pháp giải
Viết các vectơ dạng \(\overrightarrow {AX} \) (\(X \in {\rm{\{ }}B,C,D,E\} \)) và \(\overrightarrow {XB} \) (\(X \in {\rm{\{ }}A,C,D,E\} \))
Lời giải chi tiết
a) Các vectơ thỏa mãn là: \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AE} \)
a) Các vectơ thỏa mãn là: \(\overrightarrow {AB} ,\overrightarrow {CB} ,\overrightarrow {DB} ,\overrightarrow {EB} \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 28 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Cho hình vuông ABCD có cạnh bằng a. Tính \(\left| {\overrightarrow {AB} } \right|,\left| {\overrightarrow {AC} } \right|\)
Phương pháp giải
Tính độ dài các đoạn thẳng AB, AC của hình vuông theo a rồi kết luận
Lời giải chi tiết
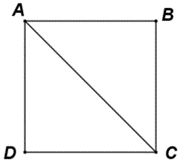
Ta có: \(\left| {\overrightarrow {AB} } \right| = AB = a\) ; \(\left| {\overrightarrow {AC} } \right| = AC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 29 trang 85 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng:
a) \(\overrightarrow {MN} = \overrightarrow {PA} \)
b) \(\overrightarrow {MP} = \overrightarrow {CN} \)
Phương pháp giải
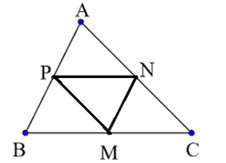
Bước 1: Chứng minh MNAP là hình bình hành rồi suy ra \(\overrightarrow {MN} = \overrightarrow {PA} \)
Bước 2: Chứng minh MPNC là hình bình hành rồi suy ra \(\overrightarrow {MP} = \overrightarrow {CN} \)
Lời giải chi tiết
a) Theo giả thiết, MN là đường trung bình của tam giác ABC \( \Rightarrow MN//AB,MN = \frac{1}{2}AB\)
mà P là trung điểm AB nên \(MN//AP,MN = AP\)
Do đó MNAP là hình bình hành \( \Rightarrow \)\(\overrightarrow {MN} = \overrightarrow {PA} \)
a) Theo giả thiết, MP là đường trung bình của tam giác ABC \( \Rightarrow MP//AC,MP = \frac{1}{2}AC\)
mà N là trung điểm AC nên \(MP//AN,MP = AN\)
Do đó MPNC là hình bình hành \( \Rightarrow \)\(\overrightarrow {MP} = \overrightarrow {CN} \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 30 trang 86 SBT Toán 10 Cánh diều tập 1 – CD
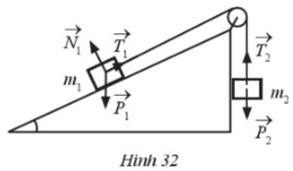
Trong mặt phẳng nghiêng không có ma sát, cho hệ vật m1, m2, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc
a) Tìm các cặp vectơ cùng phương trong các vectơ ở Hình 32
b) Những cặp vectơ cùng phương đó có cùng hướng không?
Phương pháp giải
Bước 1: Tìm các cặp vectơ có giá song song hoặc trùng nhau
Bước 2: Dựa vào hướng các vectơ cùng phương xác định các vectơ cùng hướng
Lời giải chi tiết
a) Các vectơ cùng phương là: \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \), \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{T_2}} \), \(\overrightarrow {{T_2}} \) và \(\overrightarrow {{P_2}} \)
b) Cặp vectơ \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \) cùng hướng;
2 cặp vectơ \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{T_2}} \), \(\overrightarrow {{T_2}} \) và \(\overrightarrow {{P_2}} \) ngược hướng
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
Giải bài 31 trang 86 SBT Toán 10 Cánh diều tập 1 – CD
Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\overrightarrow {AH} \) có độ dài không đổi.
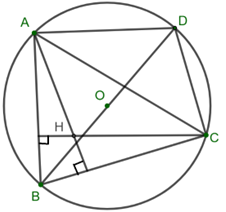
Phương pháp giải
Chứng minh AH không đổi
Bước 1: Kẻ đường kính BD của đường tròn (O)
Bước 2: Chứng minh ADCH là hình bình hành (dấu hiệu tứ giác có các cặp cạnh song song)
Bước 3: Từ giả thiết bước 2 suy ra AH = DC rồi kết luận
Lời giải chi tiết
Kẻ đường kính BD của đường tròn (O)
Ta có:
\(\widehat {BAD}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {BAD}\) = 900 \( \Rightarrow AD \bot AB\) (1)
Mặt khác, \(CH \bot AB\) (giả thiết) (2)
Từ (1) và (2) suy ra AD // CH (3)
Chứng minh tương tự ta được AH // CD (4)
Từ (3) và (4) suy ra ADCH là hình bình hành \( \Rightarrow \)AH = DC
Mà DC không đổi nên AH không đổi
\( \Rightarrow \)\(\overrightarrow {AH} \) có độ dài không đổi
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 3
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
