Giải SBT Bài 5 Chương 4 – SBT Toán 10 CÁNH DIỀU

GIẢI CHI TIẾT Giải SBT Bài 5 Chương 4 – SBT Toán 10 CÁNH DIỀU
===========

Giải bài 47 trang 99 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Sử dụng tính chất trung điểm của đoạn thẳng: AB = 2AO = 2OB và xác định hướng các vectơ tương ứng

Lời giải chi tiết

Ta có: \(\overrightarrow {AB}  = 2\overrightarrow {OB}  = 2\overrightarrow {AO} \) 

 Chọn B

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 48 trang 99 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Sử dụng tính chất đường trung tuyến trong tam giác và xác định hướng các vectơ tương ứng

Lời giải chi tiết

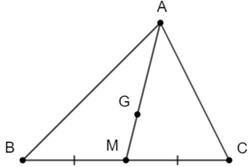
∆ABC có AM là đường trung tuyến và G là trọng tâm nên  \(AG = \frac{2}{3}AM\)  \( \Rightarrow AM = 3GM\)

Lại có G nằm giữa A và M \( \Rightarrow \overrightarrow {AM}  = 3\overrightarrow {GM} \)  

 Chọn D

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 49 trang 99 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Với số k ≠ 0, nếu k > 0 thì \(\overrightarrow a \) và \(k\overrightarrow a \) cùng hướng, nếu k < 0 thì \(\overrightarrow a \) và \(k\overrightarrow a \) ngược hướng

Lời giải chi tiết

Ta có \(\overrightarrow a \) và \(4\overrightarrow a \) cùng hướng (4 < 0)

Chọn C

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 50 trang 99 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Biểu diễn độ dài AC theo AB và xác định hướng các vectơ tương ứng

Lời giải chi tiết

Ta có: \(AC = \frac{{AC}}{{AB}}.AB\) mà C nằm giữa A và B nên \(\overrightarrow {AC}  = \frac{{AC}}{{AB}}.\overrightarrow {AB} \) 

 Chọn A

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 51 trang 99 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Biểu diễn độ dài AC theo AB và xác định hướng các vectơ tương ứng

Lời giải chi tiết

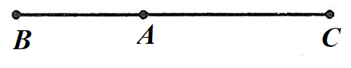
Ta có: \(AC = \frac{{AC}}{{AB}}.AB\) mà A nằm giữa C và B nên \(\overrightarrow {AC}  =  – \frac{{AC}}{{AB}}.\overrightarrow {AB} \) 

Chọn B

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 52 trang 100 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Bước 1: Xác định hướng và độ lớn các vectơ (sử dụng các quy tắc cộng, trừ, quy tắc hình bình hành,…)

Bước 2: Xác định vị trí các điểm M, N, P dựa vào hướng và độ lớn các vectơ tương ứng rồi kết luận

Lời giải chi tiết

a) Theo giả thiết, \(\overrightarrow {AM}  = \overrightarrow {CB} \)\( \Rightarrow \) \(\overrightarrow {AM} \) cùng hướng và có độ lớn bằng \(\overrightarrow {CB} \)

Vậy điểm M thuộc đường thẳng đi qua A, song song với BC sao cho AMBC là hình bình hành

 

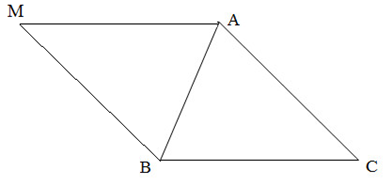
b) Theo giả thiết, \(\overrightarrow {AN}  =  – \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\)

Dựng hình bình hành ABDC, theo quy tắc hình bình hành ta có \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)\( \Rightarrow \overrightarrow {AN}  =  – \frac{1}{2}\overrightarrow {AD} \)

Vậy điểm N thuộc tia đối của tia AD thỏa mãn \(AN = \frac{1}{2}AD\)

 

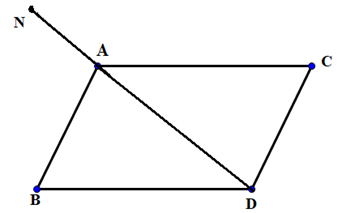
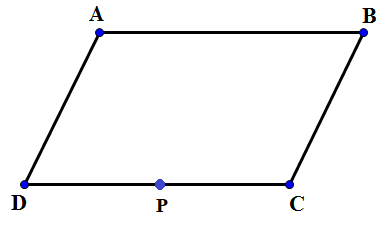
c) Theo giả thiết, \(\overrightarrow {PA}  – \overrightarrow {PB}  + 2\overrightarrow {PC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {BA}  + 2\overrightarrow {PC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {PC}  =  – \frac{1}{2}\overrightarrow {BA} \)

Dựng hình bình hành ABCD. Khi đó P là trung điểm của CD

Vậy điểm P là trung điểm đoạn thẳng CD thỏa mãn ABCD là hình bình hành

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 53 trang 100 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Bước 1: Biểu diễn độ dài DB (hoặc DC) theo DC (hoặc DB) và xác định hướng các vectơ tương ứng

Bước 2: Sử dụng định lí đường phân giác trong tam giác để biến đổi tỉ số độ dài \(\frac{{DB}}{{DC}}\)

Bước 3: Biến đổi đẳng thức ở bước 1 rồi kết luận

Lời giải chi tiết

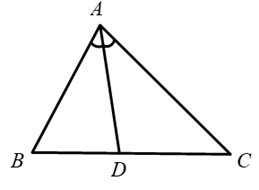
Ta có: \(DB = \frac{{DB}}{{DC}}.DC\) mà \(\overrightarrow {DB} \) và \(\overrightarrow {DC} \) ngược hướng

 \( \Rightarrow \overrightarrow {DB}  =  – \frac{{DB}}{{DC}}.\overrightarrow {DC} \)(1)

Theo giả thiết, AD là đường phân giác của ∆ABC

\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{b}{c}\) (2)

Từ (1) và (2) suy ra \(\overrightarrow {DB}  =  – \frac{c}{b}.\overrightarrow {DC}  \Leftrightarrow b\overrightarrow {DB}  =  – c\overrightarrow {DC}  \Leftrightarrow b\overrightarrow {DB}  + c\overrightarrow {DC}  = \overrightarrow 0 \) (ĐPCM)

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 54 trang 100 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Bước 1: Xác định vị trí các điểm M, N, P trên các cạnh AB, AC, AD

Bước 2: Sử dụng các quy tắc để biểu diễn các vectơ theo \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)

Bước 3: Sử dụng điều kiện \(\overrightarrow {MN}  = k\overrightarrow {NP} \) chứng minh M, N, P thẳng hàng.

Lời giải chi tiết

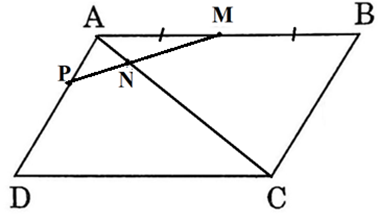
Theo giả thiết, M là trung điểm AB, N nằm giữa A và C, P nằm giữa A và D

a) Ta có:

+ \(\overrightarrow {AN}  = \frac{1}{5}\overrightarrow {AC} \). Theo quy tắc hình bình hành, \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)\)

+ \(\overrightarrow {MN}  = \overrightarrow {AN}  – \overrightarrow {AM} \)mà \(\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)\), \(\overrightarrow {AM}  = \frac{1}{2}\overrightarrow {AB}  = \frac{1}{2}\overrightarrow a \)

nên \(\overrightarrow {MN}  = \overrightarrow {AN}  – \overrightarrow {AM}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right) – \frac{1}{2}\overrightarrow a  =  – \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b \)

+ \(\overrightarrow {NP}  = \overrightarrow {AP}  – \overrightarrow {AN} \) mà \(\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)\), \(\overrightarrow {AP}  = \frac{1}{3}\overrightarrow {AD}  = \frac{1}{3}\overrightarrow b \)

nên \(\overrightarrow {NP}  = \overrightarrow {AP}  – \overrightarrow {AN}  = \frac{1}{3}\overrightarrow b  – \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right) =  – \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b \)

Vậy \(\overrightarrow {AN}  = \frac{1}{5}\left( {\overrightarrow a  + \overrightarrow b } \right)\); \(\overrightarrow {MN}  =  – \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP}  =  – \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b \) 

b) Theo a, \(\overrightarrow {MN}  =  – \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP}  =  – \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b \)  \( \Rightarrow \overrightarrow {MN}  =  – \frac{3}{{10}}\overrightarrow a  + \frac{1}{5}\overrightarrow b  = \frac{3}{2}\left( { – \frac{1}{5}\overrightarrow a  + \frac{2}{{15}}\overrightarrow b } \right) = \frac{3}{2}\overrightarrow {NP} \)

\( \Rightarrow \overrightarrow {MN} \) và \(\overrightarrow {NP} \) cùng phương. Vậy 3 điểm M, N, P thẳng hàng.

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 55 trang 100 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Bước 1: Xác định vị trí các điểm D, E, M, N trên các cạnh AB, AC, BC, AM

Bước 2: Sử dụng các quy tắc để biểu diễn các vectơ theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)

Bước 3: Sử dụng điều kiện \(\overrightarrow {EN}  = t\overrightarrow {DE} \) chứng minh D, E, N thẳng hàng.

Lời giải chi tiết

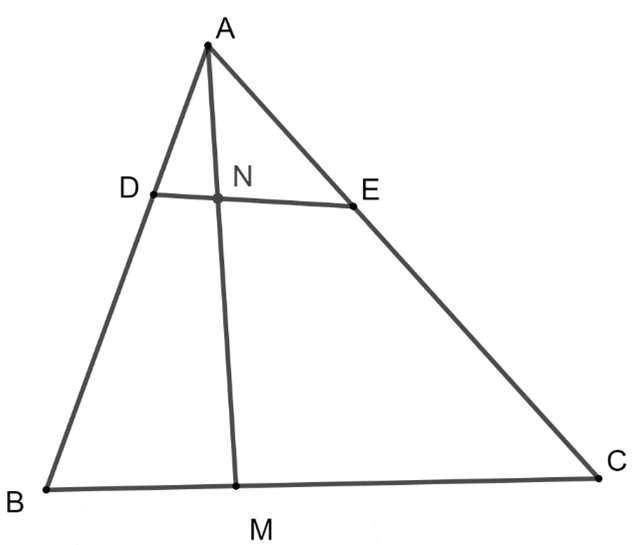
Theo giả thiết D, E, M, N nằm giữa 2 đầu mút các cạnh tương ứng AB, AC, BC, AM

a) Ta có:  \(\overrightarrow {AD}  = \frac{1}{3}\overrightarrow {AB}  = \frac{1}{3}\overrightarrow a \); \(\overrightarrow {AE}  = \frac{2}{5}\overrightarrow {AC}  = \frac{2}{5}\overrightarrow b \);

\(\overrightarrow {BM}  = \frac{1}{3}\overrightarrow {BC}  \Leftrightarrow \overrightarrow {AM}  – \overrightarrow {AB}  = \frac{1}{3}\left( {\overrightarrow {AC}  – \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM}  = \overrightarrow {AB}  + \frac{1}{3}\left( {\overrightarrow {AC}  – \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM}  = \frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b \)

+ \(\overrightarrow {AN}  = k\overrightarrow {AM}  = k\left( {\frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b } \right) = \frac{{2k}}{3}\overrightarrow a  + \frac{k}{3}\overrightarrow b \)

+ \(\overrightarrow {DE}  = \overrightarrow {AE}  – \overrightarrow {AD}  =  – \frac{1}{3}\overrightarrow a  + \frac{2}{5}\overrightarrow b \)

+ \(\overrightarrow {EN}  = \overrightarrow {AN}  – \overrightarrow {AE}  = k\left( {\frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b } \right) – \frac{2}{5}\overrightarrow b  = \frac{{2k}}{3}\overrightarrow a  + \frac{{5k – 6}}{{15}}\overrightarrow b \)

b) D, E, N thẳng hàng khi và chỉ khi \(\overrightarrow {EN}  = t\overrightarrow {DE} \) \( \Leftrightarrow \frac{{2k}}{3}\overrightarrow a  + \frac{{5k – 6}}{{15}}\overrightarrow b  = t\left( { – \frac{1}{3}\overrightarrow a  + \frac{2}{5}\overrightarrow b } \right)\)

\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{2k}}{3} =  – \frac{t}{3}\\\frac{{5k – 6}}{{15}} = \frac{{2t}}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3}k + \frac{1}{3}t = 0\\\frac{1}{3}k – \frac{2}{5}t = \frac{2}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{6}{{17}}\\t =  – \frac{{12}}{{17}}\end{array} \right.\) 

Vậy với \(k = \frac{6}{{17}}\) thì D, E, N thẳng hàng.

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5

Giải bài 56 trang 100 SBT Toán 10 Cánh diều tập 1 – CD

Phương pháp giải

Bước 1: Gọi G là trọng tâm tam giác ABC, G’ là trọng tâm tam giác A’B’C’. Biến đổi biểu thức \(\overrightarrow {AA’}  + \overrightarrow {BB’}  + \overrightarrow {CC’} \) sao cho xuất hiện vectơ \(\overrightarrow {GG’} \) (sử dụng các quy tắc vectơ)

Bước 2: Sử dụng giả thiết \(\frac{{AA’}}{{AB}} = \frac{{BB’}}{{BC}} = \frac{{CC’}}{{CA}}\)biểu diễn các vectơ \(\overrightarrow {AA’} ,\overrightarrow {BB’} ,\overrightarrow {CC’} \) theo \(\overrightarrow {AB} ,\overrightarrow {BC} ,\overrightarrow {CA} \)

Bước 3: Chứng minh \(\overrightarrow {GG’}  = \overrightarrow 0 \) rồi kết luận

Lời giải chi tiết

Gọi G là trọng tâm tam giác ABC, G’ là trọng tâm tam giác A’B’C’.

Khi đó \(\left\{ \begin{array}{l}\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \\\overrightarrow {GA’}  + \overrightarrow {GB’}  + \overrightarrow {GC’}  = \overrightarrow 0 \end{array} \right.\)

Xét \(\overrightarrow {AA’}  + \overrightarrow {BB’}  + \overrightarrow {CC’}  = \overrightarrow {AG}  + \overrightarrow {GG’}  + \overrightarrow {G’A’}  + \overrightarrow {BG}  + \overrightarrow {GG’}  + \overrightarrow {G’B’}  + \overrightarrow {CG}  + \overrightarrow {GG’}  + \overrightarrow {G’C’} \)

                             \( = \left( {\overrightarrow {AG}  + \overrightarrow {BG}  + \overrightarrow {CG} } \right) + \left( {\overrightarrow {GA’}  + \overrightarrow {GB’}  + \overrightarrow {GC’} } \right) + 3\overrightarrow {GG’}  = 3\overrightarrow {GG’} \) (1)

Mặt khác, đặt \(\frac{{AA’}}{{AB}} = \frac{{BB’}}{{BC}} = \frac{{CC’}}{{CA}} = k \Rightarrow \left\{ \begin{array}{l}AA’ = kAB\\BB’ = kBC\\CC’ = kCA\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AA’}  = k\overrightarrow {AB} \\\overrightarrow {BB’}  = k\overrightarrow {BC} \\\overrightarrow {CC’}  = k\overrightarrow {CA} \end{array} \right.\) (2)

Từ (1) và (2) suy ra \(3\overrightarrow {GG’}  = k\overrightarrow {AB}  + k\overrightarrow {BC}  + k\overrightarrow {CA}  = k\left( {\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA} } \right) = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {GG’}  = \overrightarrow 0 \)

Do đó G và G’ trùng nhau. Vậy hai tam giác ABC và A’B’C’ có cùng trọng tâm. 

 

GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 5
=======

THUỘC: Giải sách bài tập toán 10 – Cánh diều