GIẢI CHI TIẾT Giải SBT Bài 4 Chương 4 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 32 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} – \overrightarrow {NP} = \overrightarrow {MP} \)
B. \( – \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
D. \(\overrightarrow {MN} + \overrightarrow {NP} = – \overrightarrow {MP} \)
Phương pháp giải
Sử dụng quy tắc cộng hai vectơ để tìm câu đúng
Lời giải chi tiết
Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 33 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \)
B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \)
C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \)
D. \(\overrightarrow {AB} + \overrightarrow {BC} = – \overrightarrow {AC} \)
Phương pháp giải
Sử dụng quy tắc hình bình hành để tìm câu đúng
Lời giải chi tiết

Xét đáp án A: \(\overrightarrow {BA} + \overrightarrow {DA} = – \overrightarrow {AB} – \overrightarrow {AD} = – (\overrightarrow {AB} + \overrightarrow {AD} ) = – \overrightarrow {AC} = \overrightarrow {CA} \)
Chọn A
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 34 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho các điểm A, B, O. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {OA} – \overrightarrow {OB} \)
B. \(\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} \)
C. \(\overrightarrow {AB} = \overrightarrow {OA} + \overrightarrow {OB} \)
D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \)
Phương pháp giải
Sử dụng quy tắc 3 điểm để tìm câu đúng
Lời giải chi tiết
Với 3 điểm A, B, O ta có: \(\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} \)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 35 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để điểm M là trung điểm của đoạn thẳng AB là:
A. \(\overrightarrow {MA} = \overrightarrow {MB} \)
B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\)
C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng
D. \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)
Phương pháp giải
M là trung điểm AB khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)
Lời giải chi tiết
Ta có: Điều kiện cần và đủ để điểm M là trung điểm của đoạn thẳng AB là: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 36 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác ABC. Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là:
A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \)
B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)
C. \(\overrightarrow {GC} + \overrightarrow {GA} = \overrightarrow {GB} \)
D. \(\overrightarrow {GA} + \overrightarrow {GB} – \overrightarrow {GC} = \overrightarrow 0 \)
Phương pháp giải
G là trọng tâm ∆ABC khi và chỉ khi \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \). Biến đổi giả thiết để chọn câu đúng
Lời giải chi tiết
Ta có: Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = – \overrightarrow {GA} \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 37 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh \(\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} + \overrightarrow {BD} \)(*)
Phương pháp giải
Sử dụng quy tắc 3 điểm (chọn O là điểm trung gian) và trung điểm của đoạn thẳng để biến đổi một vế của (*) bằng vế còn lại
Lời giải chi tiết
Do O là trung điểm của AB nên \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \)
Biến đổi vế phải của (*) ta có:
\(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {OC} – \overrightarrow {OA} + \overrightarrow {OD} – \overrightarrow {OB} = (\overrightarrow {OC} + \overrightarrow {OD} ) – (\overrightarrow {OA} + \overrightarrow {OB} )\)
\( = (\overrightarrow {OC} + \overrightarrow {OD} ) – \overrightarrow 0 = \overrightarrow {OC} + \overrightarrow {OD} \) = Vế trái (*) (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 38 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính
a) \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\)
b) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Phương pháp giải
Bước 1: Biến đổi hiệu/ tổng 2 vectơ tương ứng thành một vectơ có giá là các cạnh của ∆ABC
Bước 2: Tính độ dài các cạnh rồi suy ra độ dài vectơ tương ứng
Bước 3: Dựng hình chữ nhật ABDC, sử dụng quy tắc hình bình hành để tính độ dài tổng 2 vectơ chung gốc
Lời giải chi tiết
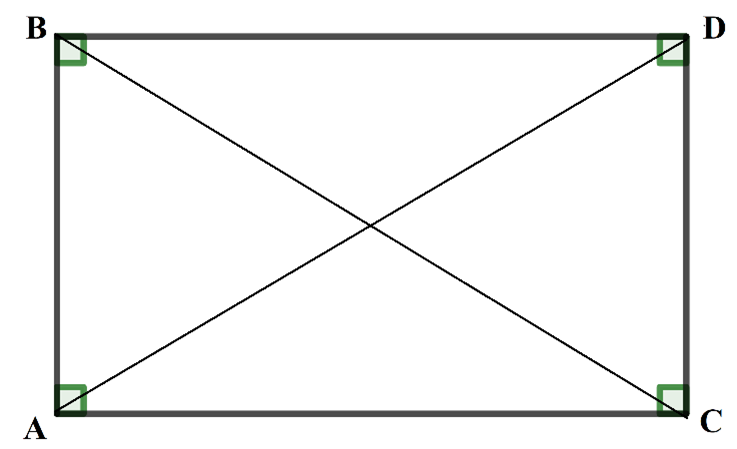
∆ABC vuông tại A, \(AB = 4a,AC = 5a\) \( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt {41} \)
a) Ta có: \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\sqrt {41} \)
b) Dựng hình chữ nhật ABCD. Khi đó \(AD = BC = a\sqrt {41} \)
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt {41} \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 39 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác đều ABC cạnh a. Tính:
a) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right|\)
b) \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\)
c) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Phương pháp giải
Bước 1: Lấy G là trọng tâm tam giác ABC
Bước 2: Sử dụng quy tắc cộng, quy tắc trừ, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi và tính độ dài các vectơ tương ứng
Lời giải chi tiết
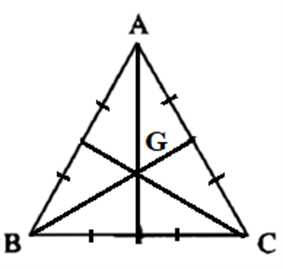
Gọi G là trọng tâm tam giác ABC
Khi đó \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \), \(GA = GB = GC = \frac{{a\sqrt 3 }}{3}\)
a) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\)
b) Ta có: \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\)
c) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\left( {\overrightarrow {GB} – \overrightarrow {GA} } \right) + \left( {\overrightarrow {GC} – \overrightarrow {GA} } \right)} \right| = \left| {\left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) – 2\overrightarrow {GA} } \right|\) (1)
Lại có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = – \overrightarrow {GA} \) (2)
Từ (1) và (2) suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| { – \overrightarrow {GA} – 2\overrightarrow {GA} } \right| = \left| { – 3\overrightarrow {GA} } \right| = 3\left| {\overrightarrow {GA} } \right| = 3GA = 3.\frac{{a\sqrt 3 }}{3} = a\sqrt 3 \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 40 trang 92 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\) (*). Chứng minh tam giác ABC vuông tại A.
Phương pháp giải
Bước 1: Dựng hình bình hành ABDC
Bước 2: Sử dụng quy tắc trừ hai vectơ và quy tắc hình bình hành để biến đổi giả thiết (*)
Bước 3: Sử dụng dấu hiệu nhận biết hình chữ nhật để chứng minh tam giác ABC vuông tại A
Lời giải chi tiết
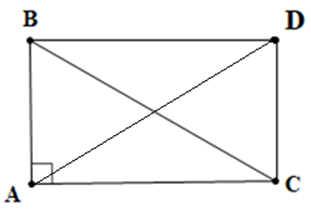
Dựng hình bình hành ABDC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| \Leftrightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right| \Leftrightarrow AD = BC\)
\( \Rightarrow \) Hình bình hành ABCD có hai đường chéo bằng nhau nên là hình chữ nhật
\( \Rightarrow \widehat {BAC} = {90^0}\). Vậy tam giác ABC vuông tại A (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 41 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Phương pháp giải
Bước 1: Dựng 2 vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) thỏa mãn \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
Bước 2: Sử dụng quy tắc cộng vectơ và độ dài vectơ để biến đổi giả thiết \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Lời giải chi tiết
![]()
Lấy một điểm A trên mặt phẳng. Dựng \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) sao cho \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
\( \Rightarrow \left| {\overrightarrow a } \right| = AB,\left| {\overrightarrow b } \right| = BC\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow {AC} \)
Lại có: AB + BC = AC \( \Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AC = \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\) (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 42 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Phương pháp giải
Dựng hình bình hành ABEC rồi biến đổi giả thiết để tính độ dài \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Lời giải chi tiết
Dựng hình bình hành ABEC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE} \)
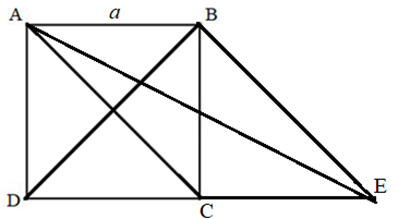
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE\)
Xét tam giác ADE vuông tại D có \(AE = \sqrt {A{D^2} + D{E^2}} = \sqrt {{a^2} + {{(2a)}^2}} = \sqrt {5{a^2}} = a\sqrt 5 \)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = AE = a\sqrt 5 \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 43 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Phương pháp giải
Bước 1: Sử dụng tính chất O là trung điểm AC, BD để tính \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
Bước 2: Chứng minh G là trọng tâm tam giác ABD rồi tính \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Lời giải chi tiết
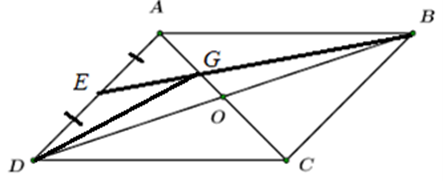
a) Do ABCD là hình bình hành nên O là trung điểm AC và BD
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \) \(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \end{array}\)
b) Xét tam giác ABD có AO và BE là hai đường trung tuyến cắt nhau tại G
\( \Rightarrow \) G là trọng tâm ∆ABD \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 44 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác ABC. Tìm tập hợp các điểm M trong mặt phẳng thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC} – \overrightarrow {AM} } \right|\)
Phương pháp giải
Sử dụng các quy tắc cộng, trừ 2 vectơ để biến đổi giả thiết rồi kết luận
Lời giải chi tiết
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC} – \overrightarrow {AM} } \right| \Leftrightarrow \left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {MC} } \right| \Leftrightarrow AM = MC\)
Vậy tập hợp các điểm M cần tìm là đường trung trực của đoạn thẳng AC
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 45 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho hai tam giác ABC và A’B’C’ có cùng trọng tâm là G. Chứng minh \(\overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} = \overrightarrow 0 \)
Phương pháp giải
Sử dụng tính chất trọng tâm tam giác, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi \(\overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} \) rồi kết luận
Lời giải chi tiết
Do G là trọng tâm tam giác ABC và tam giác A’B’C’ nên: \(\left\{ \begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\\overrightarrow {GA’} + \overrightarrow {GB’} + \overrightarrow {GC’} = \overrightarrow 0 \end{array} \right.\)
Ta có: \(\overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} = \overrightarrow {GA’} – \overrightarrow {GA} + \overrightarrow {GB’} – \overrightarrow {GB} + \overrightarrow {GC’} – \overrightarrow {GC} \)
\( = \left( {\overrightarrow {GA’} + \overrightarrow {GB’} + \overrightarrow {GC’} } \right) – \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\)\( = \overrightarrow 0 – \overrightarrow 0 = \overrightarrow 0 \) (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
Giải bài 46 trang 93 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \)
Phương pháp giải
Bước 1: Lấy E đối xứng với A qua O
Bước 2: Chứng minh các tứ giác ADEH, BHCE là hình bình hành
Bước 3: Áp dụng quy tắc hình bình hành để chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \)
Lời giải chi tiết
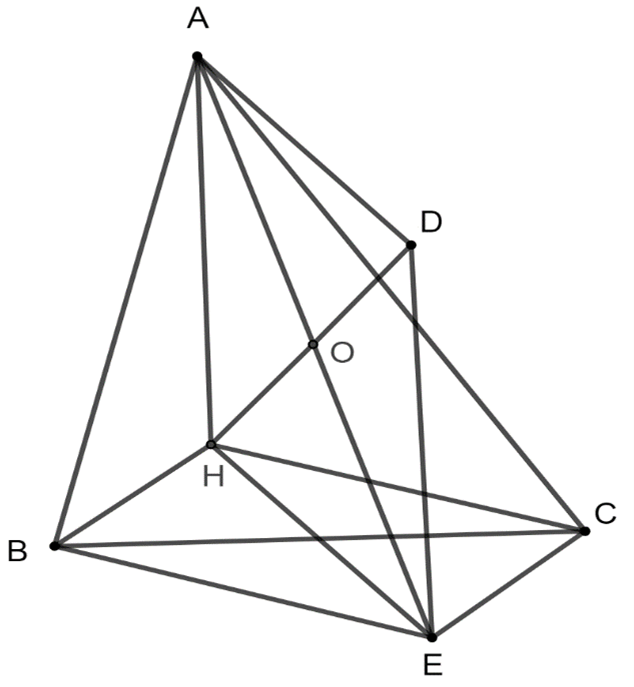
Gọi E là điểm đối xứng với A qua O . Khi đó AE là đường kính của đường tròn ngoại tiếp ∆ABC
Tứ giác ADEH có O là trung điểm HD và AE nên là hình bình hành
\( \Rightarrow \overrightarrow {HA} + \overrightarrow {HE} = \overrightarrow {HD} \)(1)
Lại có: \(\widehat {ACE}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACE} = {90^0}\)\( \Rightarrow EC \bot AC\), mà \(BH \bot AC\)
\( \Rightarrow EC//BH\)
Chứng minh tương tự ta có \(BE//HC\)
Tứ giác BHCE có \(EC//BH\), \(BE//HC\) nên là hình bình hành
\( \Rightarrow \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HE} \)(2)
Từ (1) và (2) suy ra \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HA} + \overrightarrow {HE} = \overrightarrow {HD} \) (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 4 Bài 4
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
