Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: đề thi toán 2021 bến tre

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

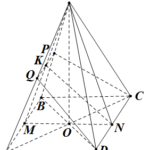
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$. Lời giải Gọi $M,N$ lần lượt là trung điểm $AB,CD. $ Khi đó $\widehat{SNM}=60^0$ là góc giữa … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$.

Đề thi mẫu HK1 Toán lớp 10 – số 2

Ngày Thuộc chủ đề:Đề thi HKI môn toán Tag với:

Đề thi mẫu HK1 Toán lớp 10 – số 2 --- 13 --- Đề bài A. PHẦN TRẮC NGHIỆM (8 điểm) Câu 1 :  Trong mặt phẳng tọa độ Oxy, cho các vectơ \(\overrightarrow u  = \left( {2; - 4} \right);\,\,\overrightarrow a  = \left( { - 1; - 2} \right);\)\(\,\,\overrightarrow b  = \left( {1; - 3} \right)\). Biết \(\overrightarrow u  = m\overrightarrow a  + n\overrightarrow b \), tính … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 2

Đề thi HK1 Toán 12 – Mẫu 4

Ngày Thuộc chủ đề:Đề thi HKI môn toán Tag với:

Đề bài Câu 1 . Số mặt phẳng đối xứng của hình chóp đều \(S.ABC\) là A.  \(4\) . B.  \(2\) . C.  \(6\) . D.   \(3\) . Câu 2 . Cho \(a\) là số thực dương khác \(1\) . Hình nào sau đây là đồ thị của hàm số mũ \(y = {a^x}\)? Câu 3 .  Khối cầu \((S)\) có bánh kính bằng \(r\) và thể tích bằng \(V\). Mệnh đề nào dưới đây đúng? A.   \(V = … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 4

Đề thi HK2 Toán 12 – Tham khảo số 5 – 2019

Ngày Thuộc chủ đề:Đề thi HKII môn toán Tag với:

Đề bài Câu 1: Tập hợp các điểm biểu diễn của z thỏa\(\left| {z - 4} \right| + \left| {z + 4} \right| = 10\) là: A.  một elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1.\) B.  một elip có phương trình \(\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{{25}} = 1.\) C.  một elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1.\) … [Đọc thêm...] vềĐề thi HK2 Toán 12 – Tham khảo số 5 – 2019

Giải bài tập Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu (Chân trời)

Ngày Thuộc chủ đề:Giải bài tập Toán 10 – Chân trời Tag với:

Giải bài tập Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu (Chân trời) Giải bài 1 trang 118 - Toán 10 CT (C6-B3) Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau: a) \(23;{\rm{ }}41;{\rm{ }}71;{\rm{ }}29;{\rm{ }}48;{\rm{ }}45;{\rm{ }}72;{\rm{ }}41\). b) \(12;{\rm{ }}32;{\rm{ }}93;{\rm{ }}78;{\rm{ }}24;{\rm{ }}12;{\rm{ }}54;{\rm{ … [Đọc thêm...] vềGiải bài tập Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu (Chân trời)

Lý thuyết Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu – Chân trời

Ngày Thuộc chủ đề:Học Toán lớp 10 – SGK Chân trời Tag với:

Lý thuyết Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu - Chân trời ============ 1.1. Số trung bình Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\) +) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là \(\overline x \), được tính bằng công thức: \(\overline x  = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\) +) Mẫu số liệu cho dưới dạng … [Đọc thêm...] vềLý thuyết Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu – Chân trời

Lý thuyết Bài 13: Các số đặc trưng đo xu thế trung tâm – Kết nối

Ngày Thuộc chủ đề:Học Toán lớp 10 – SGK Kết nối Tag với:

Lý thuyết Bài 13: Các số đặc trưng đo xu thế trung tâm ============= Tóm tắt lý thuyết 1.1. Số trung bình và trung vị a. Số trung bình Số trung bình (số trung bình cộng) của mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\), kí hiệu là \(\overline x \) được tính bằng công thức: \(\overline x  = \frac{{{x_1} + {x_2} + {x_3} + ... + … [Đọc thêm...] vềLý thuyết Bài 13: Các số đặc trưng đo xu thế trung tâm – Kết nối

Cho hai số thực \(x,\) \(y\) thỏa mãn \(0 \le x,y \le 1\) trong đó \(x,\) \(y\) không đồng thời bằng 0 hoặc 1 và \({\log _3}\left( {\frac{{x + y}}{{1 – xy}}} \right) + \left( {x + 1} \right)\left( {y + 1} \right) – 2 = 0.\) Tìm giá trị nhỏ nhất của \(P\) với \(P = 2x + y.\)

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:, ,

DẠNG TOÁN PHƯƠNG PHÁP HÀM ĐẶC TRƯNG, BIẾN ĐỔI MŨ, LOGARIT – phát triển theo đề tham khảo Toán 2021   ĐỀ BÀI: Cho hai số thực \(x,\) \(y\) thỏa mãn \(0 \le x,y \le 1\) trong đó \(x,\) \(y\) không đồng thời bằng 0 hoặc 1 và \({\log _3}\left( {\frac{{x + y}}{{1 - xy}}} \right) + \left( {x + 1} \right)\left( {y + 1} \right) - 2 = 0.\) Tìm giá trị nhỏ nhất của … [Đọc thêm...] vềCho hai số thực \(x,\) \(y\) thỏa mãn \(0 \le x,y \le 1\) trong đó \(x,\) \(y\) không đồng thời bằng 0 hoặc 1 và \({\log _3}\left( {\frac{{x + y}}{{1 – xy}}} \right) + \left( {x + 1} \right)\left( {y + 1} \right) – 2 = 0.\) Tìm giá trị nhỏ nhất của \(P\) với \(P = 2x + y.\)

Lý thuyết Khái niệm về khối đa diện

Ngày Thuộc chủ đề:Toán lớp 12 Tag với:

Lý thuyết Khái niệm về khối đa diện 1) Khối lăng trụ Hình lăng trụ: 2 đáy là 2 đa giác bằng nhau. Các cạch bên song song và bằng nhau. Các mặt bên là các hình bình hành. Khối lăng trụ  là phần không gian giới hạn bởi hình lăng trụ. Hình lăng trụ đứng: Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt … [Đọc thêm...] vềLý thuyết Khái niệm về khối đa diện