Diện tích phần hình phẳng giới hạn bởi đồ thị hai hàm số \(y = {x^3} – 3{x^2} + 2\); \(y = – {x^2} + x\) và hai đường thẳng \(x = – 1\); \(x = 2\) (phần tô màu) bằng

Diện tích phần hình phẳng giới hạn bởi đồ thị hai hàm số \(y = {x^3} – 3{x^2} + 2\); \(y = – {x^2} + x\) và hai đường thẳng \(x = – 1\); \(x = 2\) (phần tô màu) bằng

A. \(\frac{8}{3}\).

B. \(\frac{5}{{12}}\).

C. \(\frac{{37}}{{12}}\).

D. \(\frac{9}{4}\).

Lời giải:

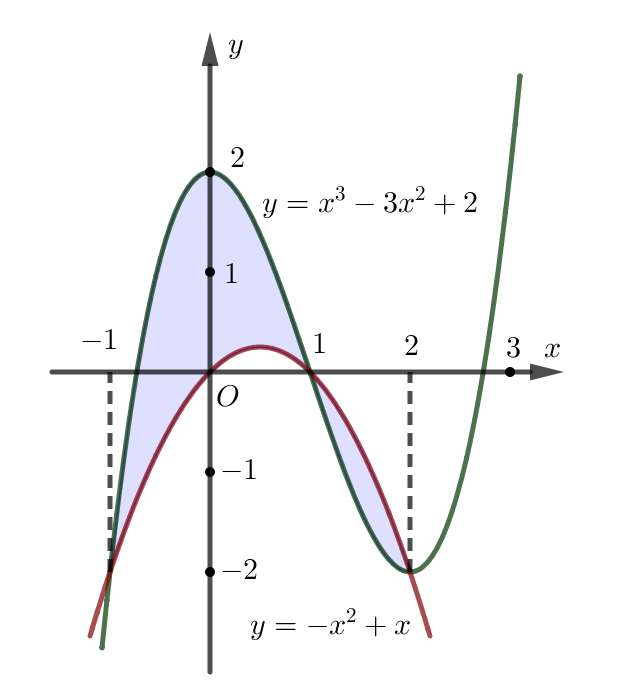
Diện tích hình phẳng cần tìm là

\(S = \int\limits_{ – 1}^2 {\left| {\left( {{x^3} – 3{x^2} + 2} \right) – \left( { – {x^2} + x} \right)} \right|{\rm{d}}x = \int\limits_{ – 1}^1 {\left( {{x^3} – 2{x^2} – x + 2} \right){\rm{d}}x – \int\limits_1^2 {\left( {{x^3} – 2{x^2} – x + 2} \right){\rm{d}}x} } } \)

\( = \left. {\left( {\frac{1}{4}{x^4} – \frac{2}{3}{x^3} – \frac{1}{2}{x^2} + 2x} \right)} \right|_{ – 1}^1 – \left. {\left( {\frac{1}{4}{x^4} – \frac{2}{3}{x^3} – \frac{1}{2}{x^2} + 2x} \right)} \right|_1^2 = \frac{{37}}{{12}}\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ NGUYÊN HAM – TICH PHÂN – ỨNG DỤNG.