Cho số phức \(z\) thỏa mãn \(\left| {\overline z – 3 + 3i} \right| = 2\), số phức \(w\) thỏa mãn \(\left| {w + 2 – i} \right| = 1\). Tìm giá trị nhỏ nhất của \(\left| {w – z} \right|\).

Cho số phức \(z\) thỏa mãn \(\left| {\overline z – 3 + 3i} \right| = 2\), số phức \(w\) thỏa mãn \(\left| {w + 2 – i} \right| = 1\). Tìm giá trị nhỏ nhất của \(\left| {w – z} \right|\).

A. \(\sqrt {21} – 3\).

B. \(\sqrt {29} + 3\).

C. \(\sqrt {29} – 3\).

D. \(\sqrt {21} + 3\).

Lời giải:

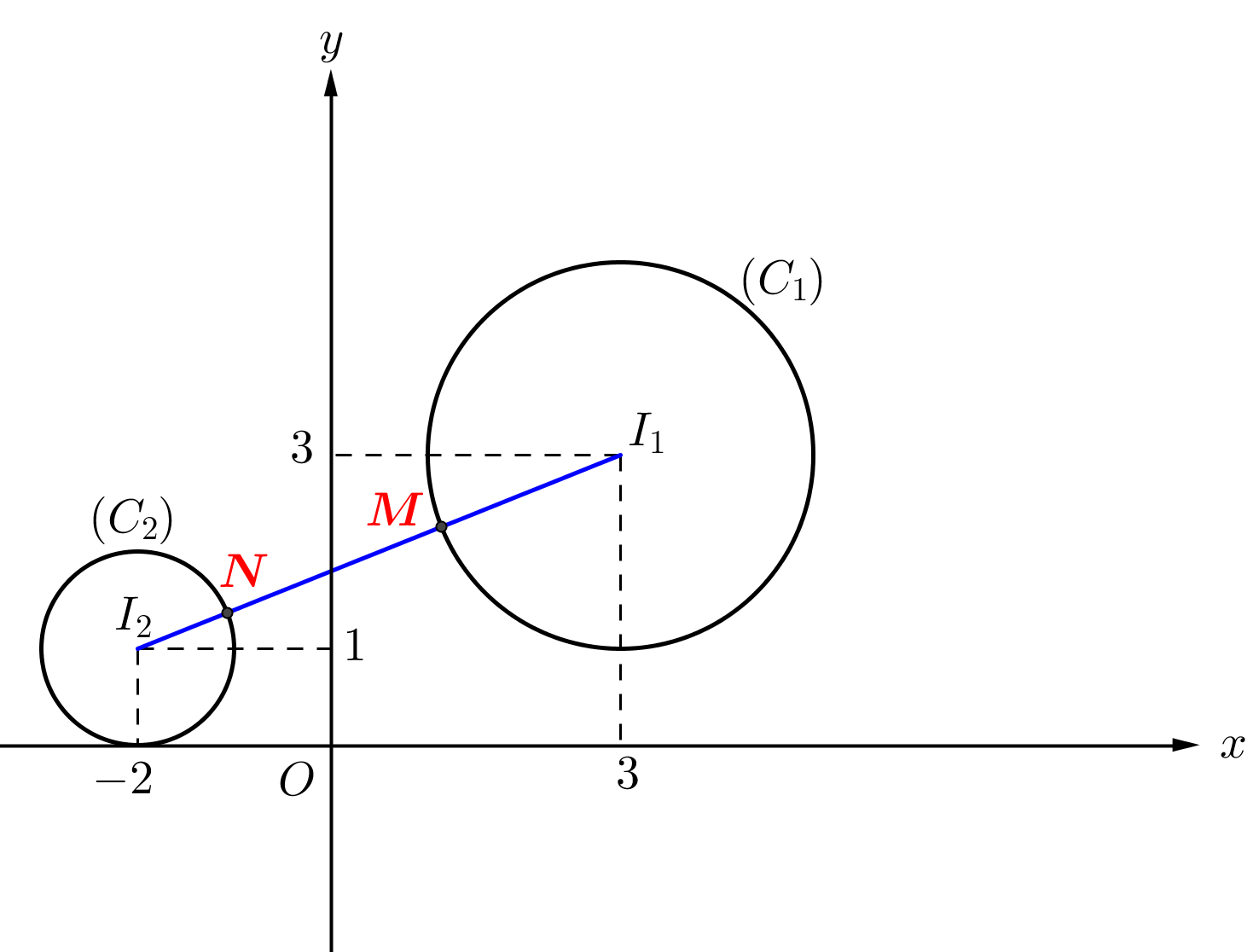
Gọi \(M\left( {x;y} \right)\) biểu diễn số phức \(z = x + yi,\left( {x,y \in \mathbb{R}} \right)\).

Ta có: \(\left| {\overline z – 3 + 3i} \right| = 2\)\( \Leftrightarrow \left| {x – yi – 3 + 3i} \right| = 2\)\( \Leftrightarrow {\left( {x – 3} \right)^2} + {\left( {y – 3} \right)^2} = 4\).

Suy ra \(M\) thuộc đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {3;3} \right)\), bán kính \({R_1} = 2\).

Gọi \(N\) biểu diễn số phức \(w\) thì \(N\) thuộc đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( { – 2;1} \right)\), bán kính \({R_2} = 1\).

\(\left| {w – z} \right| = MN\).

Giá trị nhỏ nhất của \(\left| {w – z} \right|\) chính là giá trị nhỏ nhất của đoạn \(MN\).

Ta có \(\overrightarrow {{I_1}{I_2}} = \left( { – 5; – 2} \right)\)\( \Rightarrow {I_1}{I_2} = \sqrt {29} \)\( > {R_1} + {R_2} = 3\)\( \Rightarrow \left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) ở ngoài nhau.

Do đó:\(M{N_{\min }}\)\( = {I_1}{I_2} – {R_1} – {R_2}\)\( = \sqrt {29} – 3\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Số phức.