. Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho mỗi hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng 2 cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?

Câu hỏi:
. Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho mỗi hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng 2 cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
A. \(4374\). B. \(139968\). C. \(576\). D. \(15552\).
Lời giải

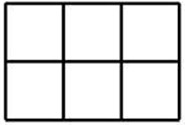
Tô màu theo nguyên tắc:
Tô \(1\) ô vuông 4 cạnh: chọn \(2\) trong \(3\) màu, ứng với \(2\) màu được chọn có \(6\) cách tô. Do đó, có \(6.C_3^2\) cách tô.
Tô \(3\) ô vuông \(3\) cạnh: ứng với 1 ô vuông có 3 cách tô màu 1 trong 3 cạnh theo màu của cạnh đã tô trước đó, chọn 1 trong 2 màu còn lại tô 2 cạnh còn lại, có \(3.C_2^1 = 6\) cách tô. Do đó có \({6^3}\) cách tô.
Tô 2 ô vuông 2 cạnh: ứng với 1 ô vuông có 2 cách tô màu 2 cạnh. Do đó có \({2^2}\) cách tô.
Vậy có: \(6.C_3^2{.6^3}.4 = 15552\) cách tô.
====================
Thuộc chủ đề: Trắc nghiệm Xác suất