Câu hỏi:
Một bộ pha trà bằng thủy tinh có bình tổng (để chứa nước trà) và các tách (chén để uống trà) đều là dạng hình trụ. Bình tổng có chiều cao gấp đôi đường kính đáy, tách trà có bán kính đáy bằng một nửa bán kính đáy bình tổng và có chiều cao bằng một phần ba chiều cao bình tổng. Có ba người ngồi thưởng trà, mỗi lượt người thưởng trà chỉ uống vừa đúng ba phần tư lượng … [Đọc thêm...] vềMột bộ pha trà bằng thủy tinh có bình tổng (để chứa nước trà) và các tách (chén để uống trà) đều là dạng hình trụ. Bình tổng có chiều cao gấp đôi đường kính đáy, tách trà có bán kính đáy bằng một nửa bán kính đáy bình tổng và có chiều cao bằng một phần ba chiều cao bình tổng. Có ba người ngồi thưởng trà, mỗi lượt người thưởng trà chỉ uống vừa đúng ba phần tư lượng nước có trong chén trà rồi lại châm thêm nước trà từ bình tổng vào chén. Hỏi sau mấy lần rót nước trà vào các chén thì hết nước trà trong bình tổng, biết rằng thể tích nước trà ban đầu có trong bình tổng chiếm ba phần tư thể tích của bình và mỗi lần rót trà thì chỉ rót vừa đủ ba phần tư thể tích của chén trà.
Một bộ pha trà bằng thủy tinh có bình tổng (để chứa nước trà) và các tách (chén để uống trà) đều là dạng hình trụ. Bình tổng có chiều cao gấp đôi đường kính đáy, tách trà có bán kính đáy bằng một nửa bán kính đáy bình tổng và có chiều cao bằng một phần ba chiều cao bình tổng. Có ba người ngồi thưởng trà, mỗi lượt người thưởng trà chỉ uống vừa đúng ba phần tư lượng nước có trong chén trà rồi lại châm thêm nước trà từ bình tổng vào chén. Hỏi sau mấy lần rót nước trà vào các chén thì hết nước trà trong bình tổng, biết rằng thể tích nước trà ban đầu có trong bình tổng chiếm ba phần tư thể tích của bình và mỗi lần rót trà thì chỉ rót vừa đủ ba phần tư thể tích của chén trà.
Que kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế.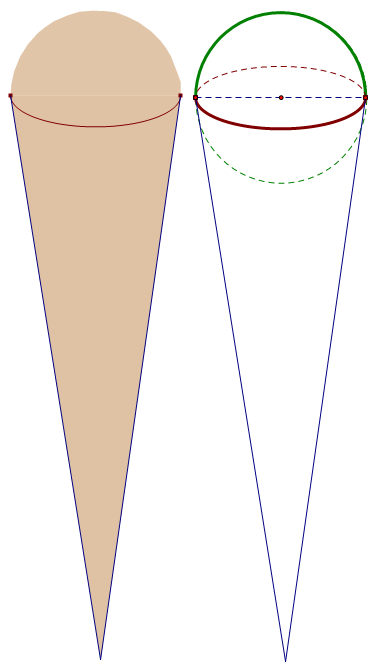
Câu hỏi:
Que kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế.
A.\(12252,21\,c{m^3}\).
B. … [Đọc thêm...] vềQue kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế.
Một tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm.
Câu hỏi:
Một tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm.
A. \(7182,13\,{{\rm{m}}^{\rm{3}}}\).
B. … [Đọc thêm...] vềMột tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm.
Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ?
Câu hỏi:
Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ?
A. \(18.850.000\) đồng.
B. \(5.441.000\) đồng.
C. \(9.425.000\) đồng. … [Đọc thêm...] vềÔng Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ?
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính \(20\;cm\) làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng \(10\;cm\). Phần phía trên làm bằng lớp vỏ kính trong suốt. Biết giá tiền của \(1\;{m^2}\) kính như trên là 1.500.000 đồng, giá triền của \(1\;{m^3}\) gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để làm đồ trang trí là bao nhiêu.
Câu hỏi:
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính \(20\;cm\) làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng \(10\;cm\). Phần phía trên làm bằng lớp vỏ kính trong suốt. Biết giá tiền của \(1\;{m^2}\) kính như trên là 1.500.000 đồng, giá triền của \(1\;{m^3}\) gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng … [Đọc thêm...] vềÔng An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính \(20\;cm\) làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng \(10\;cm\). Phần phía trên làm bằng lớp vỏ kính trong suốt. Biết giá tiền của \(1\;{m^2}\) kính như trên là 1.500.000 đồng, giá triền của \(1\;{m^3}\) gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để làm đồ trang trí là bao nhiêu.
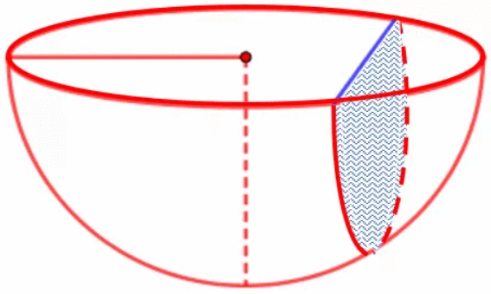
Một gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ, lòng trong của bồn tắm có hình dạng bán cầu, mất đi chỏm cầu. Biết thể tích khối chỏm cầu được tính bởi công thức \(V = \pi {h^2}\left( {R – \frac{h}{3}} \right)\) với \(R\) là bán kính khối cầu, \(h\) là chiều cao của chỏm cầu và \(OH = \frac{{\sqrt 2 }}{2}m\) . Thể tích \(\left( {{{\rm{m}}^3}} \right)\) lòng trong của bồn tắm là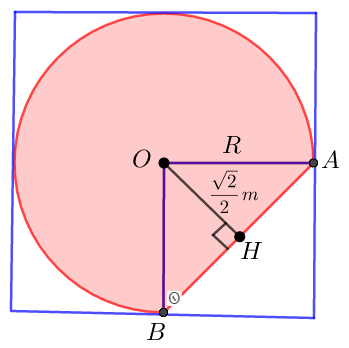
Câu hỏi:
Một gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ, lòng trong của bồn tắm có hình dạng bán cầu, mất đi chỏm cầu. Biết thể tích khối chỏm cầu được tính bởi công thức \(V = \pi {h^2}\left( {R - \frac{h}{3}} \right)\) với \(R\) là bán kính khối cầu, \(h\) là chiều cao của chỏm cầu và \(OH = \frac{{\sqrt 2 }}{2}m\) . Thể tích \(\left( {{{\rm{m}}^3}} … [Đọc thêm...] vềMột gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ, lòng trong của bồn tắm có hình dạng bán cầu, mất đi chỏm cầu. Biết thể tích khối chỏm cầu được tính bởi công thức \(V = \pi {h^2}\left( {R – \frac{h}{3}} \right)\) với \(R\) là bán kính khối cầu, \(h\) là chiều cao của chỏm cầu và \(OH = \frac{{\sqrt 2 }}{2}m\) . Thể tích \(\left( {{{\rm{m}}^3}} \right)\) lòng trong của bồn tắm là
Hình vẽ dưới đây mô tả một ngọn núi có dạng hình nón. Nhà đầu tư du lịch dự định xây dựng một con đường nhằm phục vụ việc chuyên chở khách du lịch tham quan ngắm cảnh vòng quanh ngọn núi bắt đầu từ vị trí \(A\) và dừng ở vị trí \(B\). Biết rằng người ta đã chọn xây dựng đường đi ngắn nhất vòng quanh núi từ \(A\) đến \(B\), đoạn đường đầu là phần lên dốc từ \(A\) và đoạn sau sẽ xuống dốc đến \(B\). Tính quãng đường xuống dốc khi đi từ \(A\) đến \(B\) cho biết \(AB = 15\,{\rm{m}}\), \(OA = 90\,{\rm{m}}\), bán kính đường tròn đáy nón \(R = 30\,{\rm{m}}\).
Câu hỏi:
Hình vẽ dưới đây mô tả một ngọn núi có dạng hình nón. Nhà đầu tư du lịch dự định xây dựng một con đường nhằm phục vụ việc chuyên chở khách du lịch tham quan ngắm cảnh vòng quanh ngọn núi bắt đầu từ vị trí \(A\) và dừng ở vị trí \(B\). Biết rằng người ta đã chọn xây dựng đường đi ngắn nhất vòng quanh núi từ \(A\) đến \(B\), đoạn đường đầu là phần lên dốc từ \(A\) và … [Đọc thêm...] vềHình vẽ dưới đây mô tả một ngọn núi có dạng hình nón. Nhà đầu tư du lịch dự định xây dựng một con đường nhằm phục vụ việc chuyên chở khách du lịch tham quan ngắm cảnh vòng quanh ngọn núi bắt đầu từ vị trí \(A\) và dừng ở vị trí \(B\). Biết rằng người ta đã chọn xây dựng đường đi ngắn nhất vòng quanh núi từ \(A\) đến \(B\), đoạn đường đầu là phần lên dốc từ \(A\) và đoạn sau sẽ xuống dốc đến \(B\). Tính quãng đường xuống dốc khi đi từ \(A\) đến \(B\) cho biết \(AB = 15\,{\rm{m}}\), \(OA = 90\,{\rm{m}}\), bán kính đường tròn đáy nón \(R = 30\,{\rm{m}}\).
Trong ngôi đình làng \({\rm{X}}\) có \(20\) cây cột gỗ lim hình trụ tròn. Trong số các cây cột đó có bốn cây cột lớn ở giữa có đường kính bằng \(60\,{\rm{cm}}\)và chiều cao \(4,5\,{\rm{m}}\). Các cột nhỏ còn lại đều có đường kính bằng \(40\,{\rm{cm}}\) và cây cột nhỏ có diện tích xung quanh bằng \(\frac{{16}}{{27}}\) diện tích xung quanh cây cột ở giữa. Hỏi giá của \(20\)cây cột trên là bao nhiêu (đơn vị VNĐ)? (Biết \(1{m^3}\)gỗ lim có giá \(45.000.000\)(đồng); lấy \(\pi = 3,14\)):
Câu hỏi: Trong ngôi đình làng \({\rm{X}}\) có \(20\) cây cột gỗ lim hình trụ tròn. Trong số các cây cột đó có bốn cây cột lớn ở giữa có đường kính bằng \(60\,{\rm{cm}}\)và chiều cao \(4,5\,{\rm{m}}\). Các cột nhỏ còn lại đều có đường kính bằng \(40\,{\rm{cm}}\) và cây cột nhỏ có diện tích xung quanh bằng \(\frac{{16}}{{27}}\) diện tích xung quanh cây cột ở giữa. Hỏi giá của … [Đọc thêm...] vềTrong ngôi đình làng \({\rm{X}}\) có \(20\) cây cột gỗ lim hình trụ tròn. Trong số các cây cột đó có bốn cây cột lớn ở giữa có đường kính bằng \(60\,{\rm{cm}}\)và chiều cao \(4,5\,{\rm{m}}\). Các cột nhỏ còn lại đều có đường kính bằng \(40\,{\rm{cm}}\) và cây cột nhỏ có diện tích xung quanh bằng \(\frac{{16}}{{27}}\) diện tích xung quanh cây cột ở giữa. Hỏi giá của \(20\)cây cột trên là bao nhiêu (đơn vị VNĐ)? (Biết \(1{m^3}\)gỗ lim có giá \(45.000.000\)(đồng); lấy \(\pi = 3,14\)):
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng \(9\,{\rm{cm}}\). Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.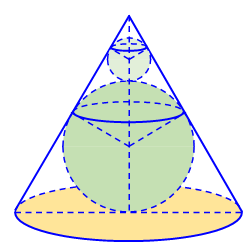
Câu hỏi:
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của … [Đọc thêm...] vềNgười ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng \(9\,{\rm{cm}}\). Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.
Một món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và \(h\) là chiều cao của chỏm cầu. Số tiền cần dùng để mạ vàng khối trang sức đó gần nhất với giá trị nào sau đây?
Câu hỏi:
Một món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và … [Đọc thêm...] vềMột món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và \(h\) là chiều cao của chỏm cầu. Số tiền cần dùng để mạ vàng khối trang sức đó gần nhất với giá trị nào sau đây?
