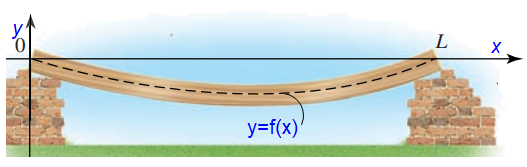
Một tấm ván gỗ chỉ được hỗ trợ ở hai đầu ${O}$ và $L$, cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục ${O x y}$ như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình ${y=f(x)}$.
Khi đó ${f^{\prime \prime}(x)=\dfrac{1}{350}\left(12 x-3 x^2\right)}$ với ${0 \leq x \leq 4}$. Hỏi tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất bao nhiêu cm (kết quả làm tròn đến hàng phần mười).
Lời giải
Trả lời: 5,7
Khoảng võng xuống lớn nhất so với phương ngang của tấm ván là bằng với ${f(x)}$ min. Do đó, ta cần đi tìm hàm ${f(x)}$. Và ta sẽ sử dụng các công thức ${\left\{\begin{array}{l}f^{\prime}(x)=\int f^{\prime \prime}(x) d x \\ f(x)=\int f^{\prime}(x) d x\end{array}\right.}$ để tìm được hàm ${f(x)}$. Thực hiện như sau:
Ta có ${f^{\prime}(x)=\int f^{\prime \prime}(x) d x=\int\left(\dfrac{1}{350}\left(12 x-3 x^2\right)\right) d x=\dfrac{1}{350}\left(\dfrac{12}{2} x^2-x^3\right)+C=\dfrac{1}{350}\left(6 x^2-x^3\right)+C}$
Tiếp đến, ta có ${f(x)=\int f^{\prime}(x) d x=\int\left(\dfrac{1}{350}\left(6 x^2-x^3\right)+C\right) {d} x=\dfrac{1}{350}\left(\dfrac{6}{3} x^3-\dfrac{x^4}{4}\right)+C x+D}$
$=\dfrac{{{x}^{3}}}{175}-\dfrac{{{x}^{4}}}{1400}+Cx+D$
Dựa vào hình vẽ, ta có $\left\{ \begin{array}{*{35}{l}}
f(0)=0 \\
f(4)=0 \\
\end{array} \right.\Leftrightarrow \left\{ \begin{array}{*{35}{l}}
D=0 \\
\dfrac{{{4}^{3}}}{175}-\dfrac{{{4}^{4}}}{1400}+4C+D=0 \\
\end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}}
D=0 \\
C=-\dfrac{8}{175} \\
\end{array} \right. \right.$
Suy ra ${f(x)=\dfrac{x^3}{175}-\dfrac{x^4}{1400}-\dfrac{8}{175} x}$.
Xét hàm số ${f(x)=\dfrac{x^3}{175}-\dfrac{x^4}{1400}-\dfrac{8}{175} x}$ trên đoạn ${[0 ; 4]}$
Ta có ${f^{\prime}(x)=\dfrac{1}{350}\left(6 x^2-x^3\right)-\dfrac{8}{175}=0 \Leftrightarrow \dfrac{1}{350}\left(6 x^2-x^3\right)=\dfrac{8}{175} \Leftrightarrow 6 x^2-x^3=16 \Leftrightarrow-x^3+6 x^2-16=0}$
$\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{*{35}{l}}
x=2-2\sqrt{3}(L) \\
x=2+2\sqrt{3}(L) \\
x=2(tm) \\
\end{array} \right. \\
f(0)=f(4)=0;f(2)=-\dfrac{2}{35}\approx -0,057. \\
\end{array}$
Vậy tấm ván bị võng xuống so với phương ngang một khoảng lớn nhất là ${0,057 {m}}$ hay ${5,7 {cm}}$.
