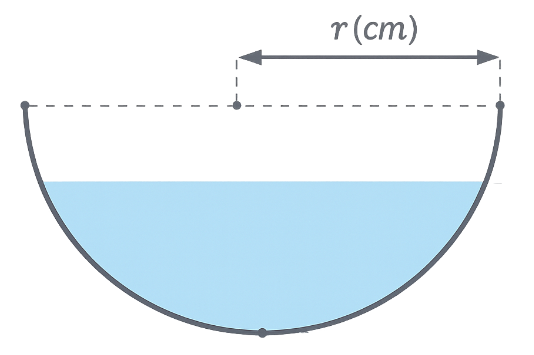
Nước bốc hơi từ một bát hình bán cầu có bán kính ${r({cm})}$ với tốc độ ${V^{\prime}(t)=-r^2}$, trong đó ${t}$ là thời gian tính bằng giờ. Giả sử bán kính của bát là ${r=10 {cm}}$ và ban đầu (lúc ${t=0}$ ) bát chứa đầy nước. Hỏi sau bao nhiêu giờ (làm tròn kết quả đến hàng phần chục) thì bát cạn nước?
Lời giải
Trả lời: 20,9
Vì bát có dạng là 1 nửa hình cầu với bán kính ${r=10 {cm}}$ nên ta có thể tích của bát khi chứa đầy nước là ${V=\dfrac{1}{2} \cdot \dfrac{4}{3} \pi \cdot 10^3=\dfrac{2000 \pi}{3}\left({cm}^3\right)}$
Theo định nghĩa nguyên hàm, ta có lượng nước trong bát là ${V(t)=\int V^{\prime}(t) d t=\int\left(-r^2\right) d t=-r^2 t+C}$.
Biết tại thời điểm ban đầu ${(t=0)}$ thì bát đầy nước nên ta có ${V(0)=\dfrac{2000 \pi}{3} \Leftrightarrow C=\dfrac{2000 \pi}{3}}$.
Suy ra ${V(t)=-10^2 t+\dfrac{2000 \pi}{3}, \quad(r=10)}$
Bát cạn nước khi ${V(t)=0 \Leftrightarrow-10^2 t+\dfrac{2000 \pi}{3}=0}$ ${\Rightarrow t \approx 20,9}$ giờ.
