Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Bài toán gốc

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

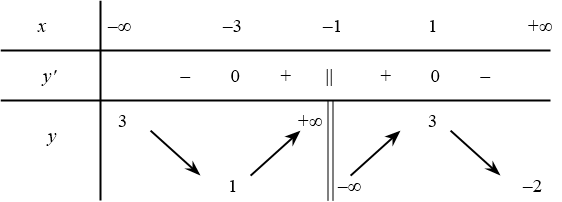
Xét tính đúng sai của các phát biểu sau:

a) Đồ thị hàm số $y=f(x)$ có một đường tiệm cận ngang.

b) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng $y=-1$.

c) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-2$.

d) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-1$.

Lời giải:
(Sai) Đồ thị hàm số $y=f(x)$ có một đường tiệm cận ngang.
(Vì): $y=3,y=-2$.
(Sai) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng $y=-1$.
(Sai) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-2$.
(Vì): Tiệm cận đứng là $x=-1$.
(Đúng) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-1$.
(Vì): Từ bảng biến thiên ta thấy thỏa điều kiện bên trái hoặc bên phải về vô cực.

Phân tích và Phương pháp giải

Dạng bài toán là xác định các đường tiệm cận (ngang và đứng) của đồ thị hàm số dựa vào bảng biến thiên (BBT). Phương pháp giải là áp dụng định nghĩa giới hạn:
– Tiệm cận ngang (TCN): Kiểm tra giới hạn của hàm số khi $x \to +\infty$ và $x \to -\infty$. Nếu $\lim_{x\to \pm\infty} f(x) = L$ ($L$ là số hữu hạn), thì $y=L$ là TCN.
– Tiệm cận đứng (TCĐ): Kiểm tra giới hạn của hàm số tại các điểm $x=a$ làm hàm số gián đoạn. Nếu $\lim_{x\to a^\pm} f(x) = \pm\infty$, thì $x=a$ là TCĐ.
Trong bài toán gốc, có 2 TCN ($y=3, y=-2$) và 1 TCĐ ($x=-1$).

Bài toán tương tự

Cho hàm số $y=f(x)$ có bảng biến thiên thể hiện các giới hạn sau:
– Khi $x \to -\infty$, $y \to 5$.
– Khi $x \to +\infty$, $y \to 1$.
– Tại $x=2$ (là điểm gián đoạn), khi $x \to 2^-$ thì $y \to +\infty$, và khi $x \to 2^+$ thì $y \to -\infty$.
Hỏi đồ thị hàm số $y=f(x)$ có tổng cộng bao nhiêu đường tiệm cận (bao gồm cả tiệm cận ngang và tiệm cận đứng)?
A. 2
B. 3
C. 4
D. 1

Đáp án đúng: B
Lời giải ngắn gọn:
– Tiệm cận ngang (TCN): Ta có $\lim_{x\to -\infty} f(x) = 5$ và $\lim_{x\to +\infty} f(x) = 1$. Do đó, đồ thị có 2 TCN là $y=5$ và $y=1$.
– Tiệm cận đứng (TCĐ): Tại $x=2$, hàm số có giới hạn vô cực, nên $x=2$ là 1 TCĐ.
Tổng số đường tiệm cận là $2 + 1 = 3$.