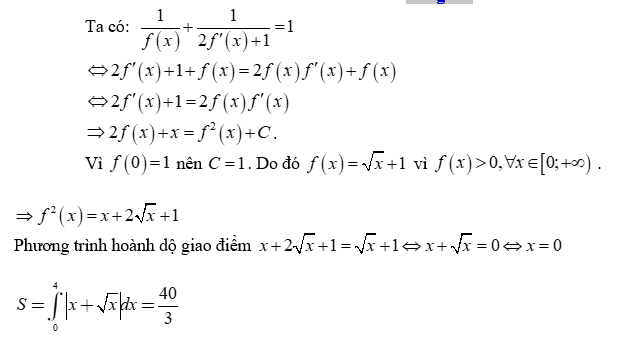
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\left[ {0; + \infty } \right)\) thỏa mãn \(f\left( 0 \right) = 1\), \(f\left( x \right) > 0,\forall x \in \left[ {0; + \infty } \right)\) và\(\frac{1}{{f\left( x \right)}} + \frac{1}{{2f’\left( x \right) + 1}} = 1,\forall x \in \left[ {0; + \infty } \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y = f(x)\) , \(y = {\left[ {f(x)} \right]^2}\) và đường thẳng \(x = 4\) bằng

Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\left[ {0; + \infty } \right)\) thỏa mãn \[f\left( 0 \right) = 1\], \[f\left( x \right) > 0,\forall x \in \left[ {0; + \infty } \right)\] và\(\frac{1}{{f\left( x \right)}} + \frac{1}{{2f’\left( x \right) + 1}} = 1,\forall x \in \left[ {0; + \infty } \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y = f(x)\) , \(y = {\left[ {f(x)} \right]^2}\) và đường thẳng \(x = 4\) bằng

A. \(\frac{{40}}{3}\).

B. \(\frac{{20}}{3}\).

C. \(\frac{{11}}{2}\).

D. \(\frac{{87}}{{35}}\).

Lời giải