GIẢI CHI TIẾT Giải SBT bài 7 Tam giác cân – Chương 7 SBT Toán 7 Cánh diều
================
Giải bài 43 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
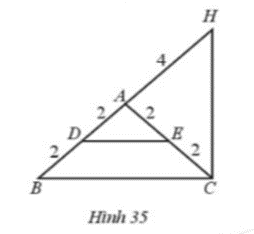
Tìm các tam giác cân trên Hình 35. Kể tên các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh của mỗi tam giác cân đó.

Phương pháp giải
Xét các tam giác cân: ADE, ABC, AHC, để xác định các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh ở các tam giác cân.
Lời giải chi tiết
|
Tên tam giác cân |
Cạnh bên |
Cạnh đáy |
Góc ở đáy |
Góc ở đỉnh |
|
∆ADE (Do AD = AE = 2) |
AD, AE |
DE |
\(\widehat {A{\rm{D}}E},\widehat {A{\rm{ED}}}\) |
\(\widehat {DA{\rm{E}}}\) |
|
∆ABC (Do AB = AC = 4) |
AB, AC |
BC |
\(\widehat {ABC},\widehat {ACB}\) |
\(\widehat {BAC}\) |
|
∆AHC (Do AC = AH = 4) |
AC, AH |
CH |
\(\widehat {ACH},\widehat {AHC}\) |
\(\widehat {HAC}\) |
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 44 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F.
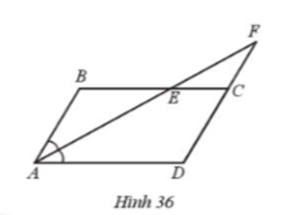
a) Chứng minh các tam giác ABE, CEF, DAF là các tam giác cân.
b) Tính số đo mỗi góc của tam giác ADF, biết \(\widehat {BAD} = 60^\circ \)
Phương pháp giải
– Chứng minh hai goác ở đáy bằng nhau suy ra tam giác cân
– Vì AB // CD nên \(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}F} = {180^o}\) và tổng ba góc trong một tam giác để tính ra số đo của mỗi góc cần tìm.
Lời giải chi tiết
a) • Vì AE là tia phân giác của \(\widehat {BAD}\) nên \(\widehat {BAE} = \widehat {EAD}\).
Vì BC // AD nên \(\widehat {BEA} = \widehat {EAD}\) (hai góc so le trong)
Do đó \(\widehat {BAE} = \widehat {BEA}\).
Suy ra tam giác ABE cân tại B.
• Vì AB // CD nên \(\widehat {BAE} = \hat F\) (hai góc so le trong).
Mà \(\widehat {BAE} = \widehat {BEA}\) chứng minh trên), \(\widehat {CEF} = \widehat {BEA}\) (hai góc đối đỉnh).
Suy ra \(\widehat {CEF} = \hat F\)
Nên tam giác CEF cân tại C.
• Ta có \(\widehat {BAF} = \widehat {{\rm{DAF}}}\) và \(\widehat {BAF} = \widehat {DFA}\) nên \(\widehat {DAF} = \widehat {DFA}\)
Do đó tam giác DAF cân tại D.
Vậy ∆ABE cân tại B, ∆CEF cân tại C, ∆DAF cân tại D.
b) Vì AB // CD nên \(\widehat {BAD} + \widehat {ADF} = 180^\circ \) (hai góc trong cùng phía)
Suy ra \(\widehat {ADF} = 180^\circ – \widehat {BAD} = 180^\circ – 60^\circ = 120^\circ \)
Xét ∆ADF có \(\widehat {ADF} + \widehat {DFA} + \widehat {DAF} = 180^\circ \) (tổng ba góc của một tam giác).
Mà \(\widehat {ADF} = 120^\circ \), \(\widehat {DAF} = \widehat {DFA}\)
Nên \(\widehat {DAF} = \widehat {DFA} = \frac{{180^\circ – \widehat {ADF}}}{2} = \frac{{180^\circ – 120^\circ }}{2} = 30^\circ \)
Vậy \(\widehat {DAF} = \widehat {DFA} = 30^\circ ,\widehat {FDA} = 120^\circ .\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 45 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
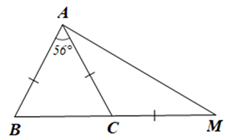
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 56^\circ \). Trên tia đối của tia CB lấy điểm M sao cho AC = CM. Tính số đo mỗi góc của tam giác ABM.
Phương pháp giải
– Sử dụng tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\).
– Tổng ba góc của 1 tam giác bằng \({180^o}\).
– Từ đó tính được số đo các góc của tam giác ABM.
Lời giải chi tiết
• Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\) (hai góc ở đáy).
Xét tam giác ABC có \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \) (tổng ba góc của một tam giác)
Do đó \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ – \widehat {BAC}}}{2} = \frac{{180^\circ – 56^\circ }}{2} = 62^\circ \)
• Ta có \(\widehat {ACB} + \widehat {ACM} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {ACM} = 180^\circ – \widehat {ACB} = 180^\circ – 62^\circ = 118^\circ \)
• Vì AC = CM (giả thiết) nên tam giác ACM cân tại C.
Suy ra \(\widehat {CAM} = \widehat {CMA}\) (hai góc ở đáy).
Xét ∆AMC có: \(\widehat {AMC} + \widehat {ACM} + \widehat {MAC} = 180^\circ \) (tổng ba góc của một tam giác).
Do đó \(\widehat {CAM} = \widehat {CMA} = \frac{{180^\circ – \widehat {ACM}}}{2} = \frac{{180^\circ – 118^\circ }}{2} = 31^\circ \)
Ta có \(\widehat {BAM} = \widehat {BAC} + \widehat {CAM} = 56^\circ + 31^\circ = 87^\circ \)
Vậy \(\widehat {BAM} = 87^\circ ,\widehat {ABM} = 62^\circ ,\widehat {AMB} = 31^\circ .\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 46 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
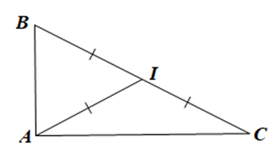
Cho tam giác ABC. Gọi I là trung điểm của BC. Tính số đo góc BAC, biết IA = IB = IC.
Phương pháp giải
– Tam giác IAB, IAC cân tại I nên suy ra các góc ở đáy bằng nhau.
– Tổng ba góc trong một tam giác bằng \({180^o}\).
– Tính số đo góc BAC.
Lời giải chi tiết
• Vì IA = IB nên tam giác IAB cân tại I.
Suy ra \(\widehat {IBA} = \widehat {IAB}\)
• Vì IA = IC nên tam giác IAC cân tại I.
Suy ra \(\widehat {IAC} = \widehat {ICA}\)
Xét ∆ABC có: \(\widehat {BAC} + \widehat {CBA} + \widehat {BCA} = 180^\circ \) (tổng ba góc của một tam giác).
Hay \(\widehat {BAC} + \widehat {IAB} + \widehat {IAC} = 2\widehat {BAC} = 180^\circ \)
Do đó \(\widehat {BAC} = 90^\circ \)
Vậy \(\widehat {BAC} = 90^\circ \)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 47 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân.
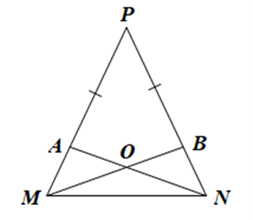
Phương pháp giải
– Sử dụng tam giác MNP cân tại P chứng minh AM = BN.
– Chứng minh: \(\Delta AMN = \Delta BNM(c – g – c)\)
– Chứng minh: \(\widehat {ONM} = \widehat {OMN}\) suy ra tam giác ONM cân tại O.
Lời giải chi tiết
Vì ∆MNP cân tại P nên ta có:
PM = PN (hai cạnh bên), \(\widehat {PMN} = \widehat {PNM}\) (hai góc ở đáy).
Ta có PM = PA + AM, PN = PB + BN.
Mà PM = PN (chứng minh trên), PA = PB (giả thiết).
Suy ra AM = BN.
Xét ∆AMN và ∆BNM có:
AM = BN (chứng minh trên),
MN là cạnh chung,
\(\widehat {AMN} = \widehat {BNM}\) (do \(\widehat {PMN} = \widehat {PNM}\))
Do đó ∆AMN = ∆BNM (c.g.c).
Suy ra \(\widehat {ANM} = \widehat {BMN}\) (hai góc tương ứng).
Hay \(\widehat {ONM} = \widehat {OMN}\)
Do đó tam giác ONM cân tại O.
Vậy tam giác OMN là tam giác cân tại O.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 48 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 120^\circ \). Trên cạnh BC lấy các điểm D, E sao cho BD = BA, CE = CA.
a) Chứng minh các tam giác BAD, CAE, AED là các tam giác cân.
b) Tính số đo mỗi góc của tam giác ADE.
Phương pháp giải
– BD = BA suy ra tam giác ABD cân tại B.
– CA = CE suy ra tam giác ACE cân tại C.
– Chứng minh: \(\widehat {A{\rm{D}}E} = \widehat {A{\rm{ED}}}\) suy ra tam giác AED cân tại A.
– Tổng ba góc trog một tam giác bằng \({180^o}\) để tính số đo mỗi góc của tam giác ADE.
Lời giải chi tiết
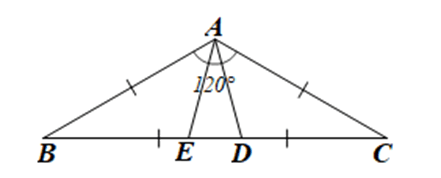
a) Vì BD = BA (giả thiết) nên tam giác ABD cân tại B.
Suy ra \(\widehat {BAD} = \widehat {BDA}\) (hai góc ở đáy).
Vì CE = CA (giả thiết) nên tam giác ACE cân tại C.
Suy ra \(\widehat {CAE} = \widehat {CEA}\) (hai góc ở đáy).
Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\)
• Xét ∆ABC có: \(\widehat {BAC} + \widehat {CBA} + \widehat {BCA} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {BAC} = 120^\circ \) (giả thiết), \(\widehat {ABC} = \widehat {ACB}\)ˆABC=ˆACBABC^=ACB^
Suy ra \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ – \widehat {BAC}}}{2} = \frac{{180^\circ – 120^\circ }}{2} = 30^\circ \)
• Xét ∆ABD có: \(\widehat {BAD} + \widehat {DBA} + \widehat {BDA} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {BAD} = \widehat {BDA}\), \(\widehat {BAD} = \widehat {BDA}\)
Suy ra \(\widehat {ADB} = \frac{{180^\circ – \widehat {ABD}}}{2} = \frac{{180^\circ – 30^\circ }}{2} = 75^\circ \)
• Xét ∆ACE có: \(\widehat {ACE} + \widehat {AEC} + \widehat {CAE} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {CAE} = \widehat {CEA}\), \(\widehat {CAE} = \widehat {CEA}\)
Suy ra \(\widehat {AEC} = \frac{{180^\circ – \widehat {ACE}}}{2} = \frac{{180^\circ – 30^\circ }}{2} = 75^\circ \).
Xét tam giác ADE có \(\widehat {ADE} = \widehat {AED}\) (cùng bằng 75°).
Suy ra tam giác AED cân tại A.
Vậy ∆ABD cân tại B, ∆ACE cân tại C và ∆AED cân tại A.
b) Xét ∆ADE có: \(\widehat {ADE} + \widehat {AED} + \widehat {DAE} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {DAE} = 180^\circ – \widehat {ADE} – \widehat {AED} = 180^\circ – 75^\circ – 75^\circ = 30^\circ \)
Vậy ∆ADE có \(\widehat {ADE} = \widehat {AED} = 75^\circ ,\widehat {EAD} = 30^\circ .\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 49 trang 83 SBT Toán 7 Cánh diều tập 2 – CD
Cho Hình 37 có AB = AC = BC = BD = CE, \(\widehat {ABD} = \widehat {ACE} = 90^\circ \)
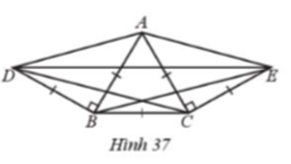
a) Chứng minh tam giác AED là tam giác cân.
b) Tính số đo các góc của tam giác ADE.
c) Chứng minh DC = BE
Phương pháp giải
– Chứng minh: AD = AE suy ra tam giác AED cân tại A.
– Sử dụng tam giác cân và tổng ba góc bằng \({180^o}\) để tính số đo góc của tam giác ADE.
– Chứng minh: \(\Delta B{\rm{D}}C = \Delta CEB(c – g – c)\) suy ra DC = BE.
Lời giải chi tiết
a) Xét ∆ABD và ∆ACE có:
\(\widehat {ABD} = \widehat {ACE} = 90^\circ \) (giả thiết),
AB = AC (giả thiết),
BD = CE (giả thiết).
Do đó ∆ABD = ∆ACE (hai cạnh góc vuông)
Suy ra AD = AE (hai cạnh tương ứng).
Nên tam giác AED cân tại A.
Vậy tam giác AED cân tại A.
b) • Vì AB = AC = BC (giả thiết) nên tam giác ABC đều.
Suy ra \(\widehat {ABC} = \widehat {ACB} = \widehat {BAC} = 60^\circ \).
Vì AC = CE , \(\widehat {ACE} = 90^\circ \) (giả thiết) nên tam giác ACE vuông cân tại C.
Suy ra \(\widehat {CEA} = \widehat {CAE} = \frac{{180^\circ – 90^\circ }}{2} = 45^\circ \)
Vì AB = BD , \(\widehat {ABD} = 90^\circ \) (giả thiết) nên tam giác ABD vuông cân tại B.
Suy ra \(\widehat {BAD} = \widehat {BDA} = \frac{{180^\circ – 90^\circ }}{2} = 45^\circ \)
Ta có \(\widehat {DAE} = \widehat {DAB} + \widehat {BAC} + \widehat {CAE} = 45^\circ + 60^\circ + 45^\circ = 150^\circ \)
• Vì tam giác AED cân tại A nên \(\widehat {ADE} = \widehat {AED}\)
Xét ∆ADE có: \(\widehat {ADE} + \widehat {AED} + \widehat {DAE} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {EAD} = 150^\circ \), \(\widehat {ADE} = \widehat {AED}\)
Suy ra \(\widehat {ADE} = \widehat {AED} = \frac{{180^\circ – 150^\circ }}{2} = 15^\circ \)
Vậy ∆ADE có \(\widehat {ADE} = \widehat {AED} = 15^\circ ,\widehat {EAD} = 150^\circ \)
c) Ta có \(\widehat {DBC} = \widehat {ABC} + \widehat {ABD} = 60^\circ + 90^\circ = 150^\circ \) ; \(\widehat {BCE} = \widehat {ACB} + \widehat {ACE} = 60^\circ + 90^\circ = 150^\circ \)
Xét ∆CBD và ∆BCE có:
BC là cạnh chung,
\(\widehat {B{\rm{D}}C} = \widehat {BCE}\) (cùng bằng 150°),
BD = CE (giả thiết),
Do đó ∆BDC = ∆CEB (c.g.c).
Suy ra DC = EB (hai cạnh tương ứng)
Vậy DC = BE.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 50 trang 84 SBT Toán 7 Cánh diều tập 2 – CD
Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều.
Phương pháp giải
Chứng minh: DE = EF = FD suy ra tam giác DEF đều.
Lời giải chi tiết
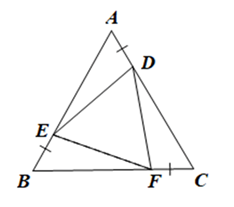
Vì tam giác ABC đều (giả thiết)
Nên AB = BC = AC và \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = 60^\circ \)
Ta có AB = AE + BE, AC = AD + DC, BC = BF + FC
Mà AB = BC = AC, AD = CF = BE.
Suy ra AE = BF = CD.
• Xét ∆ADE và ∆BEF có:
AD = BE (giả thiết),
\(\widehat {DAE} = \widehat {FBE}\) (cùng bằng 60°),
AE = BF (chứng minh trên).
Do đó ∆ADE = ∆BEF (c.g.c).
Suy ra DE = EF (hai cạnh tương ứng) (1)
• Xét ∆CFD và ∆BEF có:
CF = BE (giả thiết),
\(\widehat {FCD} = \widehat {EBF}\) (cùng bằng 60°),
CD = BF (chứng minh trên).
Do đó ∆CFD = ∆BEF (c.g.c).
Suy ra FD = EF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra DE = EF = FD.
Do đó tam giác DFE đều.
Vậy tam giác DEF là tam giác đều.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
Giải bài 51 trang 84 SBT Toán 7 Cánh diều tập 2 – CD
Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC. Biết OD = OE. Chứng minh tam giác ABC là tam giác cân.
Phương pháp giải
Chứng minh: \(\widehat {ABC} = \widehat {ACB}\) suy ra tam giác ABC cân tại A.
Lời giải chi tiết
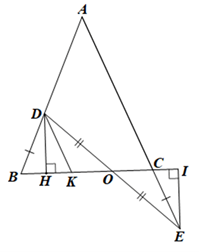
Qua D vẽ DK // AC (K ∈ BC) nên \(\widehat {KDO} = \widehat {OEC}\) (hai góc so le trong).
Xét DOKD và DOCE có:
\(\widehat {KDO} = \widehat {OEC}\) (chứng minh trên),
OD = OE (giả thiết),
\(\widehat {DOK} = \widehat {EOC}\) (hai góc đối đỉnh).
Do đó ∆OKD = ∆OCE (g.c.g).
Suy ra KD = CE (hai cạnh tương ứng).
Mặt khác BD = CE suy ra DB = DK hay tam giác DBK cân tại D.
Suy ra \(\widehat {DBK} = \widehat {DKB}\) (1)
Do DK // AC nên \(\widehat {DKB} = \widehat {ACB}\) (hai góc đồng vị) (2)
Từ (1) và (2) ta có: \(\widehat {ABC} = \widehat {ACB}\)
Suy ra tam giác ABC cân tại A.
Vậy tam giác ABC là tam giác cân tại A.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 7
=============
