GIẢI CHI TIẾT Giải SBT bài 6 Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc – Chương 7 SBT Toán 7 Cánh diều
================
Giải bài 37 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
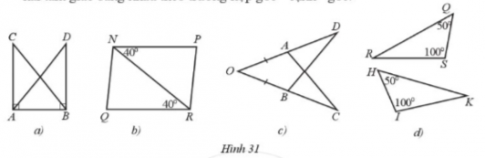
Nêu thêm một điều kiện để hai tam giác trong mỗi hình 31a, 31b, 31c, 31d là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.

a) ∆CAB = ∆DBA (Hình 31a).
b) ∆NRQ = ∆RNP (Hình 31b).
c) ∆OAC = ∆OBD (Hình 31c).
d) ∆SRQ = ∆IKH (Hình 31d).
Phương pháp giải
Quan sát các hình để thêm các điều biện bằng nhau của tam giác theo trường hợp goc – cạnh – góc
Lời giải chi tiết
a) Hình a
Để ∆CAB = ∆DBA theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh AB là cạnh chung và \(\widehat {CAB} = \widehat {DBA}\left( { = 90^\circ } \right)\).
Mặt khác, trong ∆CAB thì cạnh AB có hai góc kề là \(\widehat {CAB}\) và \(\widehat {ABC}\);
Trong ∆DBA thì cạnh AB có hai góc kề là \(\widehat {DBA}\) và \(\widehat {BAD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {ABC} = \widehat {BAD}\)
Vậy Hình 31a cần thêm điều kiện \(\widehat {ABC} = \widehat {BAD}\) .
b) Hình b
Để ∆NRQ = ∆RNP theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh NR là cạnh chung và \(\widehat {PN{\rm{R}}} = \widehat {{\rm{QRN}}}\left( { = 40^\circ } \right)\).
Mặt khác, trong ∆NRQ, cạnh NR có hai góc kề là \(\widehat {PNR}\) và \(\widehat {PRN}\) ;
Trong ∆RNP, cạnh NR có hai góc kề là \(\widehat {QRN}\) và \(\widehat {QNR}\)
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {PRN} = \widehat {QNR}.\)
Vậy Hình 31b cần thêm điều kiện \(\widehat {PRN} = \widehat {QNR}.\).
c) Hình c
Để ∆OAC = ∆OBD theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có OA = OB và \(\hat O\) là góc chung.
Mặt khác, trong ∆OAC, cạnh OA có hai góc kề là \(\hat O\) và \(\widehat {OAC}\);
Trong ∆OBD, cạnh OB có hai góc kề là \(\hat O\) và \(\widehat {OBD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {OAC} = \widehat {OBD}\).
Vậy Hình 31c cần thêm điều kiện \(\widehat {OAC} = \widehat {OBD}\).
d) Hình d
Để ∆SRQ = ∆IKH theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác này có \(\hat Q = \hat H\left( { = 50^\circ } \right)\) và \(\hat S = \hat I\left( { = 100^\circ } \right)\)
Mặt khác, trong ∆SRQ, \(\hat Q\) và \(\hat S\) là hai góc kề của cạnh QS;
Trong ∆IKH, \(\hat H\) và \(\hat I\) là hai góc kề của cạnh HI.
Do đó điều kiện còn lại là điều kiện về cạnh, đó là QS = HI.
Vậy Hình 31d cần thêm điều kiện QS = HI.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
Giải bài 38 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
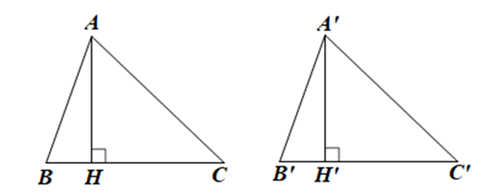
Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H’.
Phương pháp giải
– Chứng minh: \(\Delta ABH = \Delta A’B’H’\) (cạnh huyền – góc nhọn)
– Suy ra: AH = A’H’.
Lời giải chi tiết
Do ∆ABC = ∆A’B’C’ (giả thiết)
Nên AB = A’B’ (hai cạnh tương ứng) và (hai góc tương ứng).
Xét ∆ABH và ∆AB’H’ có:
\(\widehat {AHB} = \widehat {A’H’B’}\left( { = 90^\circ } \right)\)
AB = A’B’ (chứng minh trên),
\(\widehat {ABH} = \widehat {A’B’H’}\) (do \(\widehat {ABC} = \widehat {A’B’C’}\))
Suy ra ∆ABH = ∆A’B’H’ (cạnh huyền – góc nhọn).
Do đó AH = A’H’ (hai cạnh tương ứng).
Vậy AH = A’H’.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
Giải bài 39 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
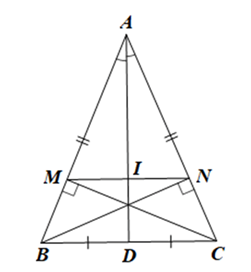
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Vẽ CM vuông góc với AB tại M, BN vuông góc với AC tại N. Chứng minh AM = AN.
Phương pháp giải
– Chứng minh \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}C(c – c – c)\) suy ra \(\widehat {ABC} = \widehat {ACB}\) hay \(\widehat {MB{\rm{D}}} = \widehat {NC{\rm{D}}}\)
– Chứng minh \(\Delta BNC = \Delta CMB\) (cạnh huyền – góc nhọn) suy ra: AB = AC và BM = CN hay
AM = AN
Lời giải chi tiết
Xét ∆ABD và ∆ACD có:
AB = AC (giả thiết),
BD = CD (do D là trung điểm của BC),
AD là cạnh chung
Do đó ∆ABD = ∆ACD (c.c.c).
Suy ra \(\widehat {ABD} = \widehat {ACD}\) hay \(\widehat {MBC} = \widehat {NCB}\).
Xét ∆BMC và ∆CNB có:
\(\widehat {BMC} = \widehat {CNB}\left( { = 90^\circ } \right)\)
BC là cạnh chung,
\(\widehat {MBC} = \widehat {NCB}\) (chứng minh trên),
Do đó ∆BMC và ∆CNB (cạnh huyền – góc nhọn).
Suy ra BM = CN (hai cạnh tương ứng).
Ta có AB = AM + MB, AC = AN + NC.
Mà AB = AC, BM = CN.
Suy ra AM = AN.
Vậy AM = AN.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
Giải bài 40 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
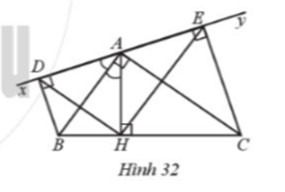
Cho Hình 32 có \(\widehat {BAC} = 90^\circ \), AH vuông góc với BC tại H, \(\widehat {xAB} = \widehat {BAH}\) , Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E. Chứng minh:
a) AC là tia phân giác của góc Hay;
b) BD + CE = BC;
c) DH vuông góc với HE.
Phương pháp giải
– Chứng minh \(\widehat {CAH} = \widehat {CAy}\) suy ra AC là tía phân giác của \(\widehat {HAy}\).
– Chứng minh: ∆ABD = ∆ABH (cạnh huyền – góc nhọn) suy ra BD = BA
Tương tự chứng minh: CH = CE
Từ đó: BC = BH + CH
Mà BD = BH, CE = CH.
Do đó BC = BD + CE.
– Gọi I là giao điểm của AB và DH
Chứng minh ∆ADI = ∆AHI (c.g.c) suy ra \(\widehat {ADI} = \widehat {AHI}\)
Tương tự chứng minh: \(\widehat {AHE} = \widehat {AEH}\)
Tính số đo góc HDE bằng \({90^o}\) nên DH vuông góc với HE
Lời giải chi tiết
a) •Ta có \(\widehat {xAy} = \widehat {xAB} + \widehat {BAC} + \widehat {CAy}\)
Hay \(180^\circ = \widehat {xAB} + 90^\circ + \widehat {CAy}\)
Suy ra \(\widehat {CAy} = 90^\circ – \widehat {xAB}\)
•Ta có \(\widehat {BAH} + \widehat {CAH} = \widehat {BAC} = 90^\circ \)
Nên \(\widehat {CAH} = 90^\circ – \widehat {BAH}\)
Mà \(\widehat {xAB} = \widehat {BAH}\) (giả thiết)
Suy ra \(\widehat {CAH} = \widehat {CAy}\)
Do đó AC là tia phân giác của \(\widehat {HAy}\)
Vậy AC là tia phân giác của \(\widehat {HAy}\) .
b) • Xét ∆ABD và ∆ABH có:
\(\widehat {ADB} = \widehat {AHB}\left( { = 90^\circ } \right)\)
AB là cạnh chung,
\(\widehat {DAB} = \widehat {HAB}\) (giả thiết),
Do đó ∆ABD = ∆ABH (cạnh huyền – góc nhọn).
Suy ra BD = BH , AD = AH (các cặp cạnh tương ứng).
• Xét ∆ACE và ∆ACH có:
\(\widehat {AEC} = \widehat {AHC}\left( { = 90^\circ } \right)\)
AC là cạnh chung,
\(\widehat {CAH} = \widehat {CAE}\) (chứng minh câu a),
Do đó ∆ACE = ∆ACH (cạnh huyền – góc nhọn).
Suy ra CE = CH, AE = AH (các cặp cạnh tương ứng).
•Ta có BC = BH + CH
Mà BD = BH, CE = CH.
Do đó BC = BD + CE.
Vậy BC = BD + CE.
c) Gọi I là giao điểm của AB và DH, K là giao điểm của EH và AC.
• Xét ∆ADI và ∆AHI có:
AD = AH (chứng minh câu b),
\(\widehat {DAI} = \widehat {HAI}\) (do \(\widehat {xAB} = \widehat {BAH}\)),
AI là cạnh chung.
Do đó ∆ADI = ∆AHI (c.g.c).
Suy ra \(\widehat {ADI} = \widehat {AHI}\) (hai góc tương ứng).
Hay \(\widehat {ADH} = \widehat {AHD}\).
• Xét ∆AHK và ∆AEK có:
AH = AE (chứng minh câu b),
\(\widehat {HAK} = \widehat {EAK}\) (do \(\widehat {HAC} = \widehat {EAC}\)),
AK là cạnh chung
Do đó ∆AHK = ∆AEK (c.g.c)
Suy ra \(\widehat {AHK} = \widehat {AEK}\) (hai góc tương ứng).
Hay \(\widehat {AHE} = \widehat {AEH}\).
Xét ∆ADH có: \(\widehat {ADH} + \widehat {AHD} + \widehat {HAD} = 180^\circ \) (tổng ba góc của một tam giác).
Mà \(\widehat {ADH} = \widehat {AHD}\) nên \(\widehat {AHD} = \frac{{180^\circ – \widehat {HAD}}}{2}\)
Xét ∆AEH có: \(\widehat {AEH} + \widehat {AHE} + \widehat {HAE} = 180^\circ \) (tổng ba góc của một tam giác)
Mà \(\widehat {AHE} = \widehat {AEH}\) nên \(\widehat {AHE} = \frac{{180^\circ – \widehat {HAE}}}{2}\)
Ta có
\(\widehat {DHE} = \widehat {AHD} + \widehat {AHE} = \frac{{180^\circ – \widehat {HAD}}}{2} + \frac{{180^\circ – \widehat {HAE}}}{2} = \frac{{{{360}^o} – \left( {\widehat {HA{\rm{D}}} + \widehat {HA{\rm{E}}}} \right)}}{2} = \frac{{{{360}^o} – {{180}^o}}}{2} = {90^o}\)
Suy ra DH vuông góc với HE.
Vậy DH vuông góc với HE.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
Giải bài 41 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
Cho tam giác ABC có ba góc đều nhọn và ˆA=60°.A^=60°. Tia phân giác của góc ABC cắt AC tại D, tia phân giác của góc ACB cắt AB tại E. BD cắt CE tại I. Tia phân giác của góc BIC cắt BC tại F. Chứng minh:
a) \(\widehat {BIC} = 120^\circ \)
b) ∆BEI = ∆BFI;
c) BC = BE + CD.
Phương pháp giải
– Dựa tính chất tia phân giác của một góc và tổng ba góc trong một tam giác để chứng minh \(\widehat {BIC} = 120^\circ \)
– Xét các điều kiện về cạnh, về góc để chứng minh ∆BEI = ∆BFI (g – c – g)
– Từ các tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau dẫn tới chứng minh BC = BE + CD.
Lời giải chi tiết
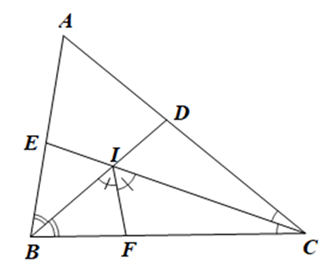
a) Vì BD là phân giác của góc ABC nên \(\widehat {ABD} = \widehat {CBD} = \frac{{\widehat {ABC}}}{2}\)
Vì CE là phân giác của góc ACB nên \(\widehat {ACE} = \widehat {ECB} = \frac{{\widehat {ACB}}}{2}\)
Xét ∆ABC có: \(\hat A + \widehat {ABC} + \widehat {ACB} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra\(\widehat {ABC} + \widehat {ACB} = 180^\circ – \hat A = 180^\circ – 60^\circ = 120^\circ \)
Xét ∆IBC có: \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \) (tổng ba góc của một tam giác)
Hay \(\widehat {BIC} + \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = 180^\circ \)
Suy ra \(\widehat {BIC} = 180^\circ – \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = 180^\circ – \frac{{120^\circ }}{2} = 120^\circ \)
Vậy \(\widehat {BIC} = 120^\circ .\)
b) Vì IF là phân giác của góc BIC nên \(\widehat {BIF} = \widehat {CIF} = \frac{{\widehat {BIC}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Ta có \(\widehat {BIC} + \widehat {BIE} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BIE} = 180^\circ – \widehat {BIC} = 180^\circ – 120^\circ = 60^\circ \)
Xét ∆BEI và ∆BFI có:
\(\widehat {EBI} = \widehat {FBI}\) (chứng minh câu a),
BI là cạnh chung,
\(\widehat {EIB} = \widehat {FIB}\) (cùng bằng 60°),
Do đó ∆BEI = ∆BFI (g.c.g).
Vậy ∆BEI = ∆BFI.
c) Do ∆BEI = ∆BFI (câu b) nên BE = BF (hai cạnh tương ứng).
Ta có \(\widehat {BIC} + \widehat {CID} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {CID} = 180^\circ – \widehat {BIC} = 180^\circ – 120^\circ = 60^\circ \)
Xét ∆CFI và ∆CDI có:
\(\widehat {FCI} = \widehat {DCI}\) (chứng minh câu a),
CI là cạnh chung,
\(\widehat {CIF} = \widehat {CID}\) (cùng bằng 60°),
Suy ra ∆CFI = ∆CDI (g.c.g).
Do đó CF = CD (hai cạnh tương ứng).
Ta có: BC = BF + FC = BE + CD.
Vậy BC = BE + CD.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
Giải bài 42 trang 81 SBT Toán 7 Cánh diều tập 2 – CD
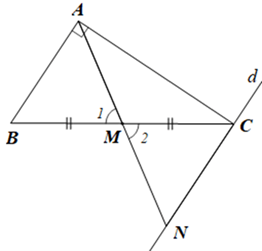
Cho tam giác ABC có \(\hat A = 90^\circ \), M là trung điểm của BC. Chứng minh BC = 2AM.
Phương pháp giải
– Chứng minh \(\Delta MBA = \Delta MCN(g – c – g)\)
Suy ra: AB = CN và AM = MN
– Chứng minh: \(\Delta BAC = \Delta NCA\) từ đó chứng minh được BC = 2AM
Lời giải chi tiết
Qua C kẻ đường thẳng d song song với AB, d cắt AM tại N.
Suy ra \(\widehat {ABC} = \widehat {BCN}\) (hai góc so le trong).
Ta có BA ⊥ AC, d // AB.
Suy ra d ⊥ AC hay \(\widehat {NCA} = 90^\circ \)
Xét ∆MBA và ∆MCN có:
BM = CM (vì M là trung điểm của BC),
\({\hat M_1} = {\hat M_2}\) (hai góc đối đỉnh),
\(\widehat {ABC} = \widehat {NCB}\) (chứng minh trên)
Do đó ∆MBA = ∆MCN (g.c.g).
Suy ra AB = CN và AM = NM (các cặp cạnh tương ứng).
Xét ∆BAC và ∆NCA có:
AC là cạnh chung,
\(\widehat {BAC} = \widehat {NCA}\) (cùng bằng 90o),
AB = NC (chứng minh trên)
Do đó ∆BAC = ∆NCA (c.g.c)
Suy ra BC = NA (hai cạnh tương ứng).
Mà AM = MN, AN = AM + MN = 2AM.
Nên BC = AN = 2AM.
Vậy 2AM = BC.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 6
=============
