GIẢI CHI TIẾT Giải SBT bài 4 Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh – Chương 7 SBT Toán 7 Cánh diều
================
Giải bài 27 trang 75 SBT Toán 7 Cánh diều tập 2 – CD
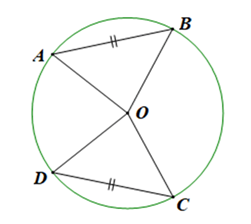
Cho bốn điểm A, B, C, D nằm trên đường tròn tâm O sao cho AB = CD. Chứng minh \(\widehat {AOB} = \widehat {COD}\)
Phương pháp giải
Xét các điều kiện các cạnh để chứng minh \(\Delta OAB = \Delta 0C{\rm{D}}(c – c – c)\) suy ra \(\widehat {AOB} = \widehat {CO{\rm{D}}}\)
Lời giải chi tiết

Vì bốn điểm A, B, C, D nằm trên đường tròn tâm O nên OA = OB = OC = OD.
Xét ∆OAB và ∆OCD có:
AO = OC (chứng minh trên),
AB = DC (giả thiết),
OB = OD (chứng minh trên),
Suy ra ∆OAB = ∆OCD (c.c.c).
Do đó \(\widehat {AOB} = \widehat {CO{\rm{D}}}\) (hai góc tương ứng).
Vậy \(\widehat {AOB} = \widehat {CO{\rm{D}}}\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 4
Giải bài 28 trang 75 SBT Toán 7 Cánh diều tập 2 – CD
Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ một phần đường tròn tâm C và tâm D có cùng bán kính, E là điểm chung của hai phần đường tròn đó (E nằm trong góc xOy) (Hình 15).
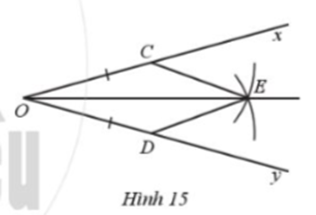
Vẽ các đoạn thẳng CE, DE. Chứng minh:
a) ΔOCE = ΔODE;
b) OE là tia phân giác của góc xOy;
c) \(\widehat {OCE} = \widehat {ODE}\)
Phương pháp giải
Xét các điều kiện về cạnh để chứng minh ΔOCE = ΔODE (c- c- c) từ đó suy ra các góc tương ứng bằng nhau nên OE là tia phân giác của góc xOy và \(\widehat {OCE} = \widehat {ODE}\)
Lời giải chi tiết
a) Vì E là điểm chung của hai phần đường tròn tâm C, tâm D có cùng bán kính nên EC = ED.
Xét ΔOCE và ΔODE có:
EC = ED (chứng minh trên),
OC = OD (giả thiết),
OE là cạnh chung.
Suy ra ΔOCE = ΔODE (c.c.c).
Vậy ΔOCE = ΔODE.
b) Vì ΔOCE = ΔODE(chứng minh câu a).
Nên \(\widehat {COE} = \widehat {DOE}\) (hai góc tương ứng).
Suy ra OE là tia phân giác của góc xOy.
Vậy OE là tia phân giác của góc xOy.
c) Vì ∆OCE = ∆ODE (chứng minh câu a)
Nên \(\widehat {OCE} = \widehat {ODE}\) (hai góc tương ứng).
Vậy \(\widehat {OCE} = \widehat {ODE}\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 4
Giải bài 29 trang 75 SBT Toán 7 Cánh diều tập 2 – CD
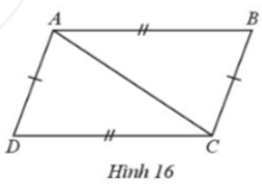
Ở Hình 16 có AB = CD, AD = BC. Chứng minh:
a) AB song song CD;
b) \(\widehat {ABC} = \widehat {A{\rm{D}}C}.\)
Phương pháp giải
Xét các điều kiện về cạnh để chứng minh \(\Delta ABC = \Delta C{\rm{D}}A\) suy ra các góc tương ứng bằng nhau từ đó chứng minh AB song song CD và \(\widehat {ABC} = \widehat {A{\rm{D}}C}\)
Lời giải chi tiết
a) Xét ΔABC và ΔCDA có:
AB = CD (giả thiết),
BC = AD (giả thiết),
AC là cạnh chung.
Suy ra ∆ABC = ∆CDA (c.c.c).
Do đó \(\widehat {BAC} = \widehat {DCA}\) (hai góc tương ứng).
Mà góc BAC và góc ACD ở vị trí so le trong
Do đó AB // CD.
Vậy AB // CD.
b) Vì ∆ABC = ∆CDA (chứng minh câu a).
Suy ra \(\widehat {ABC} = \widehat {CDA}\) (hai góc tương ứng).
Vậy \(\widehat {ABC} = \widehat {CDA}\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 4
Giải bài 30 trang 75 SBT Toán 7 Cánh diều tập 2 – CD
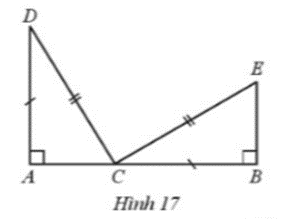
Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC; DC = CE. Chứng minh:
a) ΔDAC = ΔCBE;
b) \(\widehat {DCE} = 90^\circ \).
Phương pháp giải
– Xét các điều kiện về cạnh để chứng minh hai tam giác vuông DAC và CDE bằng nhau trong trường hợp cạnh huyền – cạnh góc vuông.
– Từ ΔDAC = ΔCBE suy ra \(\widehat D = \widehat {BCE}\). Tính được số đo góc BCE.
Lời giải chi tiết
a) Xét ∆ACD và ∆BEC có:
\(\widehat {CAD} = \widehat {EBC}\) (cùng bằng 90°),
CD = CE (giả thiết),
AD = BC (giả thiết).
Do đó ΔDAC = ΔCBE (cạnh huyền – cạnh góc vuông).
Vậy ΔDAC = ΔCBE.
b) Vì ΔDAC = ΔCBE (chứng minh câu a)
Suy ra \(\widehat {DCA} = \widehat {CEB}\) (cặp góc tương ứng).
Xét ΔCEB vuông tại B có: \(\widehat {CEB} + \widehat {ECB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {DCA} + \widehat {ECB} = 90^\circ \)
Mặt khác \(\widehat {DCA} + \widehat {DCB} = 180^\circ \) (hai góc kề bù)
Hay \(\widehat {DCA} + \widehat {DCE} + \widehat {ECB} = 180^\circ \)
Suy ra \(\widehat {DCE} = 180^\circ – \left( {\widehat {DCA} + \widehat {ECB}} \right) = 180^\circ – 90^\circ = 90^\circ \)
Vậy \(\widehat {DCE} = 90^\circ .\)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 4
=============
