Đề: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, D là trung điểm BC. Biết SAD là tam giác đều và mặt phẳng (SAD) vuông góc với mặt phẳng (ABC). Tính khoảng cách từ C đến mặt phẳng (SAB).

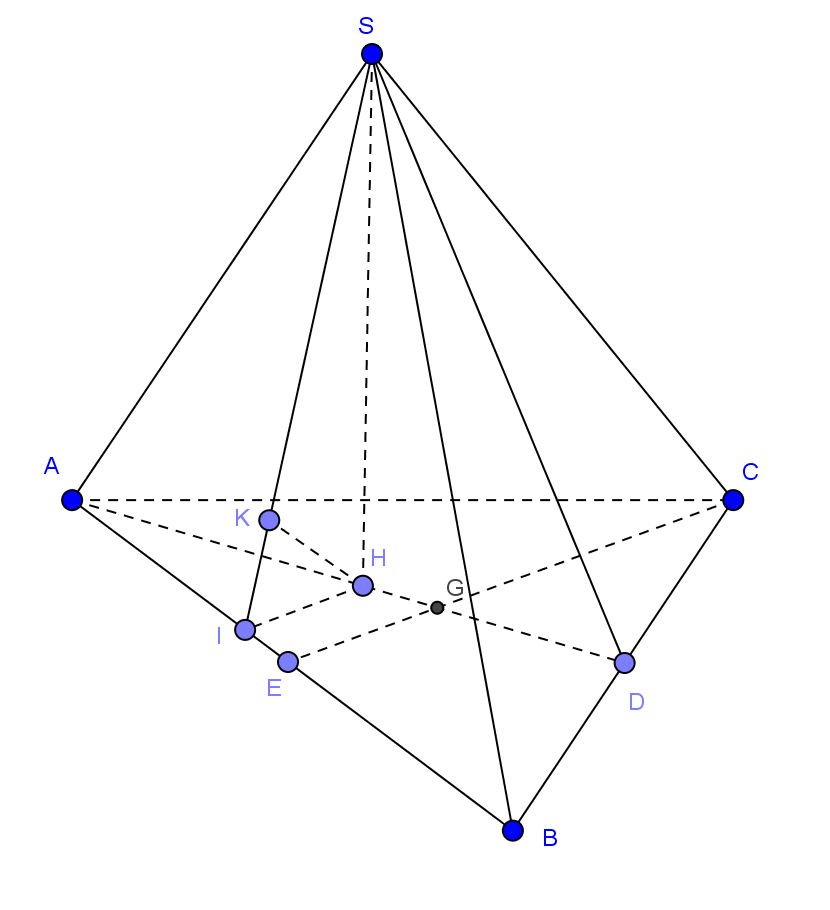
Gọi H là trung điểm của \(AD \Rightarrow SH \bot \left( {ABC} \right)\)

Ta có: \(AD = \sqrt {{{\left( {2a} \right)}^2} – {a^2}}  = a\sqrt 3 ;SH = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} – {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}  = \frac{{3a}}{2}\)

Gọi E là trung điểm của AB. Qua H kẻ đường thẳng song song với CE, giao với AB tại I.

Kẻ \(KH \bot SI\). Ta có: \(KH \bot \left( {SAB} \right)\)

Ta có: \(CE = AD = a\sqrt 3 ;EG = \frac{{CE}}{3} = \frac{{a\sqrt 3 }}{3};\frac{{AH}}{{AG}} = \frac{3}{4}\)

\(\frac{{HI}}{{EG}} = \frac{{AH}}{{AG}} = \frac{3}{4} \Rightarrow HI = \frac{3}{4}EG = \frac{3}{4}.\frac{{a\sqrt 3 }}{3} = \frac{{a\sqrt 3 }}{4}\)

\(\frac{1}{{K{H^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{1}{{{{\left( {\frac{{3a}}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}}} = \frac{{52}}{{9{a^2}}} \Rightarrow HK = \frac{{3a}}{{2\sqrt {13} }}\)

Ta có \(HI = \frac{3}{4}EG = \frac{3}{4}.\frac{1}{3}CE = \frac{1}{4}CE \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = 4d\left( {H;\left( {SAB} \right)} \right) = 4.\frac{{3a}}{{2\sqrt {13} }} = \frac{{6a}}{{\sqrt {13} }}\)