Toán lớp 12

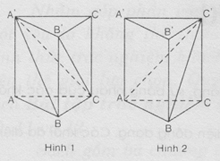
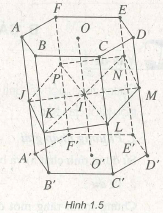
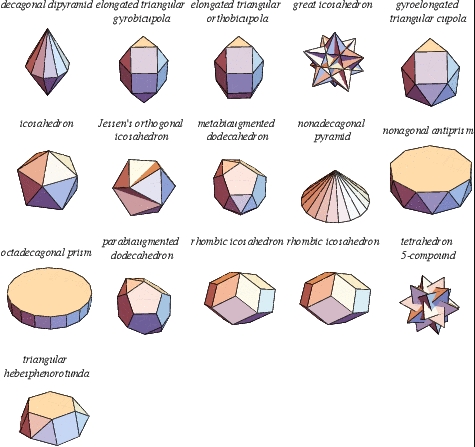
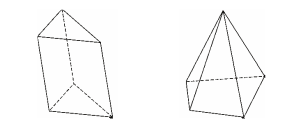
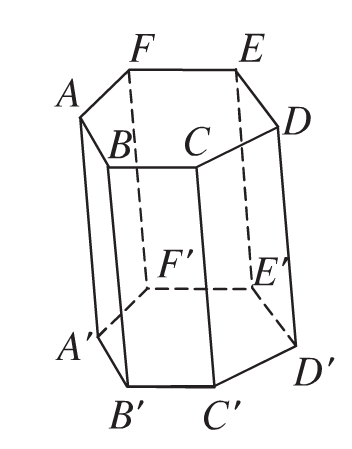
Phân chia và lắp ghép khối đa diện Việc phân chia và lắp ghép các khối đa diện thường được sử dụng để tính toán các yếu tố như thể tích, diện tích của những khối đa diện phức tạp. Có nhiều cách để phân chia một khối đa diện thành các khối đa diện khác như tứ diện, hình chóp,... Phương pháp giải Chọn mặt phẳng thích hợp để phân chia khối đa diện. Trong nhiều … [Đọc thêm...] vềPhân chia và lắp ghép khối đa diện

♦ Vấn đề 1: Chứng minh một số tính chất liên quan đến các đỉnh, các cạnh,, các mặt của một khối đa diện 1. Phương pháp giải Sử dụng tính chất a) và b) trong định nghĩa hình đa diện. 2. Ví dụ Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của đúng ba mặt thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ. Giải Gọi d là số các đỉnh của … [Đọc thêm...] vềVí dụ minh họa khái niệm khối đa diện

Khối đa diện là gì? (đọc thêm) 1. Hình đa diện (gọi tắt là đa diện) (H) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai điều kiện: a) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung. b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Mỗi đa giác như thế được gọi là một mặt của … [Đọc thêm...] vềKhối đa diện là gì?

Lý thuyết Khái niệm về khối đa diện 1) Khối lăng trụ Hình lăng trụ: 2 đáy là 2 đa giác bằng nhau. Các cạch bên song song và bằng nhau. Các mặt bên là các hình bình hành. Khối lăng trụ  là phần không gian giới hạn bởi hình lăng trụ. Hình lăng trụ đứng: Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt … [Đọc thêm...] vềLý thuyết Khái niệm về khối đa diện