Lý thuyết Khối đa diện lồi và khối đa diện đều

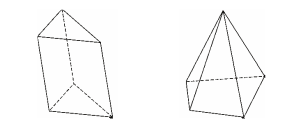
1. Khối đa diện lồi

• Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.

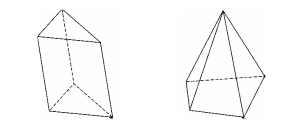
• Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.

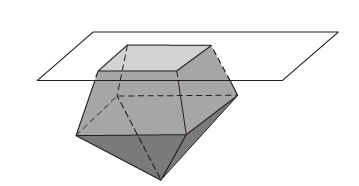
2. Khối đa diện đều

• Một khối đa diện lồi được gọi là khối đa diện đều loại {p,q} nếu:
  • Mỗi mặt của nó là một đa giác đều p cạnh.
  • Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

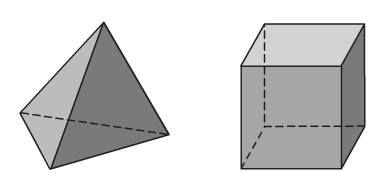
• Các mặt của khối đa diện đều là những đa giác đều và bằng nhau.
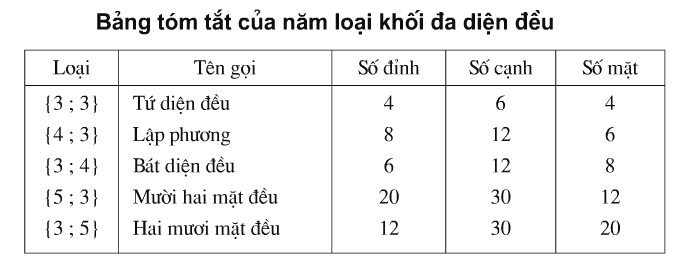
• Có năm loại khối đa diện đều. Đó là các khối đa diện đều loại {3,3}, loại {4,3}, loại {3,4}, loại {5,3}, và loại {3,5}.

Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo theo thứ tự được gọi là khối đa diện đều, khối lập phương, khối tám mặt đều, khối mười hai mặt đều, khối hai mươi mặt đều.

• Hai khối đa diện đều có cùng số mặt và có cạnh bằng nhau thì bằng nhau.
• Hai khối đa diện đều có cùng số mặt thì đồng dạng với nhau.

Công thức tính số đỉnh, số cạnh của \(m\) mặt đều loại \((n;p)\)

Vì mỗi mặt có \(n\) cạnh và 2 mặt chung một cạnh nên có:

Số cạnh \( = \frac{{m.n}}{2}\)

Vì mỗi mặt có \(n\) đỉnh và \(p\) mặt chung một đỉnh nên có:

Số đỉnh \( = \frac{{m.n}}{p}\)

Giải câu hỏi SGK Hình học 12.

Giải câu hỏi 1 trang 15 SGK Hình học 12.

Đề bài

Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.

Lời giải chi tiết

Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic

Khối đa diện không lồi trong thực tế: cái bàn

Giải câu hỏi 2 trang 16 SGK Hình học 12.

Đề bài

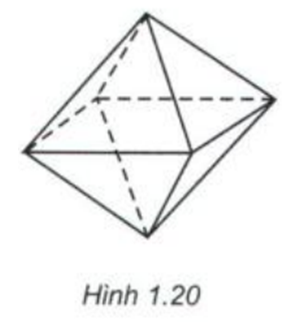
Đếm số đỉnh, số cạnh của khối bát diện đều.

Lời giải chi tiết

Khối bát diện đều có 6 đỉnh và 12 cạnh.

===========

Giải câu hỏi 3 trang 17 SGK Hình học 12.

Đề bài

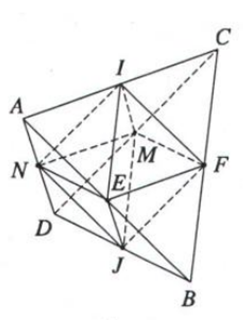
Chứng minh rằng tam giác IEF, IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng \({a \over 2}\)

Lời giải chi tiết

ABCD là tứ diện đều ⇒ tam giác ABC đều ⇒ AB = BC = CA = a

I, E, F lần lượt là trung điểm của các cạnh AC, AB, BC nên ta có IE, IF, EF là các đường trung bình của tam giác ABC

\(\eqalign{
& \Rightarrow IE = {1 \over 2}BC = {1 \over 2}a \cr
& {\rm{IF = }}{1 \over 2}AB = {1 \over 2}a \cr
& {\rm{EF = }}{1 \over 2}AC = {1 \over 2}a \cr} \)

Nên tam giác IEF là tam giác đều cạnh bằng \({a \over 2}\)

Chứng minh tương tự ta có: IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng \({a \over 2}\)