Hình học không gian

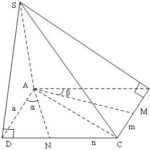
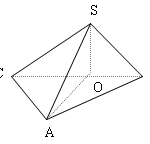
Đề bài: Trong mặt phẳng ($P$) cho hình vuông $ABCD$ có cạnh bằng $a, S$ là một điểm bất kì nằm trên đường thẳng $At $ vuông góc với mặt phẳng $(P$) tại $A$.$1.$ Tính theo $a$ thể tích hình cầu ngoại tiếp hình chóp $S.ABCD$ khi $SA = 2a$.$2$. $M, N$ lần lượt là hai điểm di động trên các cạnh $CB, CD (M \in CB ;\,\,N \in CD)$ và đặt $CM = m, CN = n$. Tìm một biểu thức liên hệ … [Đọc thêm...] vềĐề bài: Trong mặt phẳng ($P$) cho hình vuông $ABCD$ có cạnh bằng $a, S$ là một điểm bất kì nằm trên đường thẳng $At $ vuông góc với mặt phẳng $(P$) tại $A$.$1.$ Tính theo $a$ thể tích hình cầu ngoại tiếp hình chóp $S.ABCD$ khi $SA = 2a$.$2$. $M, N$ lần lượt là hai điểm di động trên các cạnh $CB, CD (M \in CB ;\,\,N \in CD)$ và đặt $CM = m, CN = n$. Tìm một biểu thức liên hệ giữa $m$ và $n$ để các mặt phẳng $(SMA)$ và $(SAN)$ tạo với nhau một góc ${45^0}$

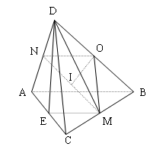
Đề bài: Cho tứ diện $ABCD.$Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,AD$$a.$ Hãy tính cosin của góc giữa $AB,DM$ biết $ABCD$ là tứ diện đều có cạnh bằng $a$$b.$ Hãy tính góc giữa $AB,CD$ biết $AB=CD=2a$ và $MN=a\sqrt{3} $ Lời giải $a.$ Gọi $E$ là trung điểm của $AC$ ta có :$EM//AB$ và $EM=\frac{a}{2} $do đó $(AB,DM)=(MD,ME)$Xét $\Delta DEM$ ta có … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD.$Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,AD$$a.$ Hãy tính cosin của góc giữa $AB,DM$ biết $ABCD$ là tứ diện đều có cạnh bằng $a$$b.$ Hãy tính góc giữa $AB,CD$ biết $AB=CD=2a$ và $MN=a\sqrt{3} $

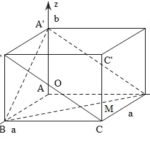
Đề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=a, AA'=b(a>0,b>0)$. Gọi $M$ là trung điểm cạnh $CC'$a) Tính thể tích khối tứ diện $BDA'M$ theo $a$ và $b$b) Xác định tỉ số $\frac{a}{b} $ để hai mặt phẳng $(A'BD)$ và $(MBD)$ và vuông góc với nhau Lời giải a) Chọn hệ trục tọa độ $Oxyz$ như sau:- Gốc $O\equiv A$- Trục $Ox$ … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=a, AA'=b(a>0,b>0)$. Gọi $M$ là trung điểm cạnh $CC'$a) Tính thể tích khối tứ diện $BDA'M$ theo $a$ và $b$b) Xác định tỉ số $\frac{a}{b} $ để hai mặt phẳng $(A'BD)$ và $(MBD)$ và vuông góc với nhau

Đề bài: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$$a)$ Hãy dựng mặt phẳng $(P)$ đi qua $A$ song song với đường thẳng $BC$ và vuông góc với mặt phẳng $(SBC)$$b)$ Giả sử góc giữa mặt phẳng $(P)$ và mặt đáy là $\alpha$.Gọi $M$ là trung điểm cạnh $BC$.Tính $SM$ theo $a$ và $\alpha$ Lời giải a)  Theo đinh nghĩa của hình chóp đều, dễ thấy $AM,SM$ cung vuông góc với … [Đọc thêm...] vềĐề bài: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$$a)$ Hãy dựng mặt phẳng $(P)$ đi qua $A$ song song với đường thẳng $BC$ và vuông góc với mặt phẳng $(SBC)$$b)$ Giả sử góc giữa mặt phẳng $(P)$ và mặt đáy là $\alpha$.Gọi $M$ là trung điểm cạnh $BC$.Tính $SM$ theo $a$ và $\alpha$

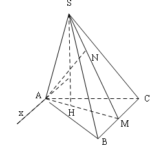
Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ Lời giải $a.$ Gọi $O$ là trung điểm của $BC$ suy ra $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$Ngoài ra theo giả thiết ta có : $SA=SB=SC$ nên  $SO$ là trục … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$

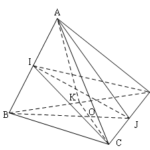
Đề bài: Cho tứ diện đều $ABCD$ có cạnh bằng $a.$Gọi $I,J,K$ lần lượt là trung điểm của $AB,CD,BD$$a.$ Chứng minh rằng $(ABJ)$ là mặt phẳng trung trực của $CD$, đồng thời mặt phẳng này tạo với hai mặt phẳng $(CAB),(DAB)$ hai góc bằng nhau.$b,$ Tính số đo của góc tạo bởi $mp(ACK)$ và $mp(ABJ)$ Lời giải $a.$ Các mặt của tứ diện là các tam giác đều, nên $AJ,BJ$ cùng … [Đọc thêm...] vềĐề bài: Cho tứ diện đều $ABCD$ có cạnh bằng $a.$Gọi $I,J,K$ lần lượt là trung điểm của $AB,CD,BD$$a.$ Chứng minh rằng $(ABJ)$ là mặt phẳng trung trực của $CD$, đồng thời mặt phẳng này tạo với hai mặt phẳng $(CAB),(DAB)$ hai góc bằng nhau.$b,$ Tính số đo của góc tạo bởi $mp(ACK)$ và $mp(ABJ)$

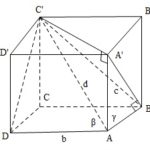
Đề bài: Cho $\alpha, \beta, \gamma$ là ba góc tạo bởi đường chéo hình hộp chữ nhật với ba cạnh xuất phát từ một điểm. Chứng minh:a) $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$b) $\sqrt{4cos^2\alpha+1}+\sqrt{4\cos^2\beta+1}+\sqrt{4\cos^2\gamma+1}\leq \sqrt{21}$ Lời giải a) Chứng minh: $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$Giả sử cho hình hộp chữ nhật $ABCD.A'B'C'D'$ … [Đọc thêm...] vềĐề bài: Cho $\alpha, \beta, \gamma$ là ba góc tạo bởi đường chéo hình hộp chữ nhật với ba cạnh xuất phát từ một điểm. Chứng minh:a) $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$b) $\sqrt{4cos^2\alpha+1}+\sqrt{4\cos^2\beta+1}+\sqrt{4\cos^2\gamma+1}\leq \sqrt{21}$

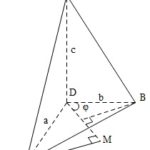
Đề bài:     Cho tứ diện $ABCD$, trong đó góc tam diện đỉnh $D$ là tam diện vuông. Giả sử $DA=a, DB=b, DC=c$. Chứng minh rằng với mỗi điểm $M$ nằm trên một cạnh  của $\triangle ABC$ thì:    $S=d(A,DM)+d(B,DM)+d(C,DM) \leq \sqrt{2(a^2+b^2+c^2)}$Khi nào xảy ra dấu bằng, ở đây $d(A,DM)$ là khoảng cách từ $A$ đến $DM$. Lời giải Không giảm tổng quát ta có thể giả sử $A$ … [Đọc thêm...] vềĐề bài:     Cho tứ diện $ABCD$, trong đó góc tam diện đỉnh $D$ là tam diện vuông. Giả sử $DA=a, DB=b, DC=c$. Chứng minh rằng với mỗi điểm $M$ nằm trên một cạnh  của $\triangle ABC$ thì:    $S=d(A,DM)+d(B,DM)+d(C,DM) \leq \sqrt{2(a^2+b^2+c^2)}$Khi nào xảy ra dấu bằng, ở đây $d(A,DM)$ là khoảng cách từ $A$ đến $DM$.

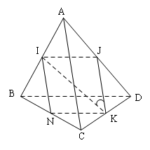
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$ Lời giải cần giải chi tiết$a.$ Tức giác $IJKN$ là hình bình hành.$JK//AC$ nên góc giữa … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$