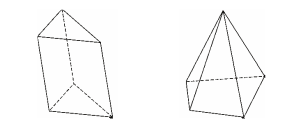
Trong hình học, một khối đa diện đều là một khối đa diện có tất cả các mặt là các đa giác đều bằng nhau và các cạnh bằng nhau. Đa diện đều được chia thành đa diện đều lồi và lõm. Đa diện đều lồi Trong không gian ba chiều, có đúng 5 khối đa diện đều lồi, chúng là các khối đa diện duy nhất (xem chứng minh trong bài) có tất cả các mặt, các cạnh và các góc ở đỉnh bằng nhau. … [Đọc thêm...] vềKhối đa diện đều là gì?
Kết quả tìm kiếm cho: ty so
Ví dụ minh họa Khối đa diện lồi và khối đa diện đều
Ví dụ minh họa Khối đa diện lồi và khối đa diện đều Xem lý thuyết đa diện đều Câu 1: Số cạnh của tứ diện đều là bao nhiêu? Hướng dẫn: Tứ diện đều thuộc loại \({\rm{\{ 3;3\} }}\) nên số cạnh bằng \(\frac{{4 \times 3}}{2} = 6\) Câu 2: Khối đa diện đều loại {4;3} có bao nhiêu mặt Hướng dẫn: Đây là khối lập phương nên có 6 mặt. Câu 3: Khối đa diện đều loại … [Đọc thêm...] vềVí dụ minh họa Khối đa diện lồi và khối đa diện đều
Lý thuyết Khối đa diện lồi và khối đa diện đều
1. Khối đa diện lồi Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi. Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó. 2. Khối đa diện đều Một khối đa diện lồi … [Đọc thêm...] vềLý thuyết Khối đa diện lồi và khối đa diện đều
Sự tương giao của đồ thị
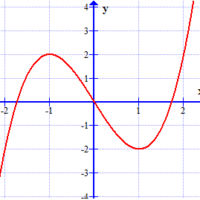
Sự tương giao của đồ thị - Sự tương giao của đường cong... Sự tương giao của hai đồ thị: Hoành độ giao điểm của 2 đồ thị hàm số $y = f(x)$ và $y = g(x)$ là nghiệm của phương trình: $$f(x) = g(x), \ \ \ (*)$$ Từ đó suy ra số giao điểm của hai đồ thị đã cho bằng số nghiệm của phương trình $(*)$. ------------- 1. Dựa vào đồ thị để biện luận số nghiệm của phương trình: … [Đọc thêm...] vềSự tương giao của đồ thị
Khảo sát sự biến thiên và vẽ đồ thị của hàm nhất biến
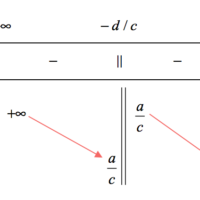
Khảo sát và vẽ đồ thị hàm nhất biến. Khảo sát và vẽ đồ thị hàm bậc nhất trên bậc nhất. Hàm nhất biến. Có dạng $y = \frac{{ax + b}}{{cx + d}},\;\;ad \ne bc.$ $\left( a \right)$ Tập xác định $D = \mathbb{R}\backslash \left\{ { - \frac{d}{c}} \right\}$. $\left( b \right)$ Giới hạn và tiệm cận: $\left( b_1 \right)$ $\mathop {\lim }\limits_{x \to {{\left( { - \frac{d}{c}} … [Đọc thêm...] vềKhảo sát sự biến thiên và vẽ đồ thị của hàm nhất biến
Khảo sát sự biến thiên và vẽ đồ thị của hàm trùng phương
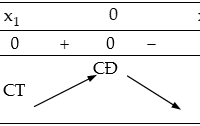
Phương pháp : Các bước khảo sát và vẽ đồ thị hàm số trùng phương $y = a{x^4} + b{x^2} + c$ với $a ≠ 0.$ + Bước 1. TXĐ: $D=\mathbb{R}.$ + Bước 2. Đạo hàm: ${y}’=4a{{x}^{3}}+2bx$ $=2x(2a{{x}^{2}}+b)$ $\Rightarrow {y}’=0\Leftrightarrow x=0$ hoặc ${{x}^{2}}=-\frac{b}{2a}$. Nếu $ab\ge 0$ thì $y$ có một cực trị ${{x}_{0}}=0.$ Nếu $ab<0$ thì $y$ có $3$ cực trị … [Đọc thêm...] vềKhảo sát sự biến thiên và vẽ đồ thị của hàm trùng phương
Ví dụ Đường tiệm cận
Phương pháp Tìm tiệm cận ngang, tiệm cận đứng của đồ thị hàm số $y = f(x)$ Thực hiện theo các bước sau: + Bước 1. Tìm tập xác định của hàm số $f(x).$ + Bước 2. Tìm các giới hạn của $f(x)$ khi $x$ dần tới các biên của miền xác định và dựa vào định nghĩa của các đường tiệm cận để kết luận. Chú ý: + Đồ thị hàm số $f$ chỉ có thể có tiệm cận ngang khi tập xác định của nó là … [Đọc thêm...] vềVí dụ Đường tiệm cận
Lý thuyết Đường tiệm cận
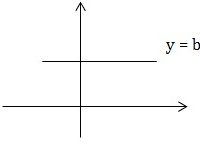
1. Đường tiệm cận ngang a) Định nghĩa Đường thẳng \(y=b\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau: \(\lim_{x\rightarrow -\infty } f(x) = b\) \(\lim_{x\rightarrow +\infty } f(x) = b\) b) Chú ý Điều kiện để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) có tiệm cận ngang là bậc của đa thức P(x) bé hơn … [Đọc thêm...] vềLý thuyết Đường tiệm cận
Đề thi thử môn toán 2018
Book Toán sưu tầm các đề thi thử môn toán của các trường trong cả nước năm 2018 để thi THPT Quốc gia 2018 tại đây: Các đề thi sẽ để thứ tự theo cập nhật mới nhất lên trên. Ưu tiên các đề có lời giải chi tiết, đáp án, file word. Các đề được sưu tập từ nhiều nguồn, nguồn trên file đính kèm. ===================== Đề thi thử môn Toán 2018 THPT chuyên Lào Cai – Lần 3 … [Đọc thêm...] vềĐề thi thử môn toán 2018
Chuyên đề 4: Giải bài toán bằng cách lập phương trình,hệ phương trình và các bài toán thực tế
I)Kiến thức cần nhớ: -Hiều đề,vững các phép biến đổi biểu thức để có thể biểu diễn ẩn và giải phương trình hoặc hệ phương trình. *Phương pháp giải: Bước 1: Lập phương trình hoặc hệ phương trình: -Chọn ẩn số,đặt điều kiện của ẩn số. -Biểu diễn các đại lượng đề bài theo ẩn số. -Lập phương trình hoặc hệ phương trình để biểu thị mối quan hệ giữa các đại lượng của đề … [Đọc thêm...] vềChuyên đề 4: Giải bài toán bằng cách lập phương trình,hệ phương trình và các bài toán thực tế