Câu hỏi: Một chất điểm chuyển động theo qui luật \(s = 6{t^2} - {t^3}\)(trong đó t là khoảng thời gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t (giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất. A.t=2 B.t=4 C.t=1 D.t=3 Hãy chọn trả lời đúng trước … [Đọc thêm...] vềĐề: Một chất điểm chuyển động theo qui luật \(s = 6{t^2} – {t^3}\)(trong đó t là khoảng thời gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t (giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất.
Kết quả tìm kiếm cho: ty so
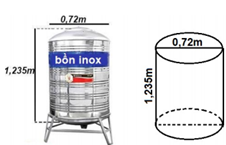
Đề: Một khối hộp chữ nhật ABCD.A1B1C1D1 có đáy ABCD là một hình vuông. Biết diện tích toàn phần của hình hộp đó là 32. Hỏi thể tích lớn nhất V của khối hộp ABCD.A1B1C1D1 là bao nhiêu?
Câu hỏi: Một khối hộp chữ nhật ABCD.A1B1C1D1 có đáy ABCD là một hình vuông. Biết diện tích toàn phần của hình hộp đó là 32. Hỏi thể tích lớn nhất V của khối hộp ABCD.A1B1C1D1 là bao nhiêu? A.\(V = \frac{{56\sqrt 3 }}{9}\) B.\(V= \frac{{70\sqrt 3 }}{9}\) C.\(V = \frac{{64\sqrt 3 }}{9}\) D.\(V = … [Đọc thêm...] vềĐề: Một khối hộp chữ nhật ABCD.A1B1C1D1 có đáy ABCD là một hình vuông. Biết diện tích toàn phần của hình hộp đó là 32. Hỏi thể tích lớn nhất V của khối hộp ABCD.A1B1C1D1 là bao nhiêu?
Đề: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ nặng \(P(n) = 480 – 20n\) (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Câu hỏi: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ nặng \(P(n) = 480 - 20n\) (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá … [Đọc thêm...] vềĐề: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ nặng \(P(n) = 480 – 20n\) (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
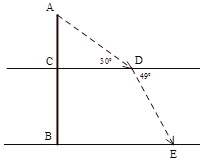
Đề: Dynamo là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynamo làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diến nào của anh chảng trẻ tuổi tài cao này đều khiến người xem há hốc miệng kinh ngạc vì nó vượt qua giới hạn của khoa học. Một lần đến New York anh ngấu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di truyển từ tòa nhà này đến toà nhà khác và trong quá trình anh di chuyển đấy có một lần anh đáp đất tại một điểm trong khoảng cách của hai tòa nhà. (Biết mọi di chuyển của anh đều là đường thẳng). Biết tòa nhà ban đầu Dynamo đứng có chiều cao là a(m), tòa nhà sau đó Dynamo đến có chiều cao là b(m) (a
Câu hỏi: Dynamo là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynamo làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diến nào của anh chảng trẻ tuổi tài cao này đều khiến người xem há hốc miệng kinh ngạc vì nó vượt qua giới hạn của khoa học. Một lần đến New York anh ngấu hứng trình diễn khả năng bay lơ lửng trong không trung của mình … [Đọc thêm...] vềĐề: Dynamo là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynamo làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diến nào của anh chảng trẻ tuổi tài cao này đều khiến người xem há hốc miệng kinh ngạc vì nó vượt qua giới hạn của khoa học. Một lần đến New York anh ngấu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di truyển từ tòa nhà này đến toà nhà khác và trong quá trình anh di chuyển đấy có một lần anh đáp đất tại một điểm trong khoảng cách của hai tòa nhà. (Biết mọi di chuyển của anh đều là đường thẳng). Biết tòa nhà ban đầu Dynamo đứng có chiều cao là a(m), tòa nhà sau đó Dynamo đến có chiều cao là b(m) (a
Toàn cảnh đề thi toán THPT Quốc gia từ 2017 đến 2019 – Giới hạn
Toàn cảnh đề thi toán THPT Quốc gia từ 2017 đến 2019 - Giới hạn ========== file word, giải chi tiết. các bạn tham khảo ôn thi 2019 =================== XEM TRỰC TUYẾN -----------------1m9OSoVV6eQVsAY4s15elR5EyUlqV4gji Đề thi file pdf DOWNLOAD file .DOC ---- ..... (Nguồn sưu tầm...) … [Đọc thêm...] vềToàn cảnh đề thi toán THPT Quốc gia từ 2017 đến 2019 – Giới hạn
Đề thi thử tuyển sinh 10 năm 2020 môn Toán TT Luyện thi ĐH KHTN
Đề thi thử tuyển sinh 10 năm 2019 môn Toán TT Luyện thi ĐH KHTN Câu 1:Mã câu hỏi: 74714 Cho Parabol \(\left( P \right):y = \frac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):y = 4 - x\). Vẽ (P) và (d) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm (P) và (d) bằng phép tính. Câu 2:Mã câu hỏi: 74715 Cho phương trình: \({x^2} - 2\left( {m - 2} … [Đọc thêm...] vềĐề thi thử tuyển sinh 10 năm 2020 môn Toán TT Luyện thi ĐH KHTN
Đề thi thử tuyển sinh lớp 10 môn Toán năm 2020 Trường THCS Bạch Đằng TP.HCM
Đề thi thử tuyển sinh lớp 10 môn Toán năm 2019 Trường THCS Bạch Đằng TP.HCM Câu hỏi trắc nghiệm (8 câu): Câu 1:Mã câu hỏi: 71402 Cho hàm số \(\left( {\rm{P}} \right){\rm{:y}} = \frac{{\rm{1}}}{{\rm{4}}}{{\rm{x}}^{\rm{2}}}\) và \(\left( {\rm{D}} \right){\rm{:y}} = \frac{{\rm{5}}}{{\rm{4}}}{\rm{x}} - {\rm{1}}\) a) Vẽ đồ thị (P) trên hệ trục tọa … [Đọc thêm...] vềĐề thi thử tuyển sinh lớp 10 môn Toán năm 2020 Trường THCS Bạch Đằng TP.HCM
Chuẩn bị vào lớp 1 Môn Toán
Chuẩn bị vào lớp 1 Môn Toán file doc Môn toán chuẩn bị vào lớp 1 được biên soạn có hệ thống. Phân loại khoa học theo từng dạng bài cụ thể. Quá trình luyện tập học sinh có thể hệ thống hóa lời giải một cách chi tiết. Quý thầy cô giáo có thể tải về dựa theo đối tượng học sinh của mình. Để sửa đổi cho phù hợp. Ngoài ra với phương pháp dạy học tích cực. thầy cô có thể đưa … [Đọc thêm...] vềChuẩn bị vào lớp 1 Môn Toán
Đề thi HK2 Toán 12 – Cần Thơ – 2019
Đề thi HK2 Toán 12 – Cần thơ – 2019 file pdf =================== XEM TRỰC TUYẾN ----------------- Đề thi file pdf DOWNLOAD file pdf ---- ..... … [Đọc thêm...] vềĐề thi HK2 Toán 12 – Cần Thơ – 2019
Đề Kiểm Tra 1 tiết chương 3 Hình học 12 – Đề 3
Đề bài Câu 1: Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \((P)\)là mặt phẳng song song với mặt phẳng \(Oxz\) và cắt mặt cầu \({(x - 1)^2} + {(y + 2)^2} + {z^2} = 12\)theo đường tròn có chu vi lớn nhất. Phương trình của \((P)\) là: A.\(x - 2y + 1 = 0\). B.\(y - 2 = 0\). C.\(y + 1 = 0\). D.\(y + 2 = 0\). Câu 2: Trong không gian với hệ trục … [Đọc thêm...] vềĐề Kiểm Tra 1 tiết chương 3 Hình học 12 – Đề 3