Đề bài Câu 1. Tìm \(I = \int {\dfrac{{{{\cos }^3}x}}{{1 + \sin x}}\,dx} \). A. \(I = - \dfrac{1}{2}{\sin ^2}x + \sin x + C\). B. \(I = \dfrac{1}{2}{\sin ^2}x + \sin x + C\). C. \(I = {\sin ^2}x - \sin x + C\) D. \(I = - \dfrac{1}{2}{\sin ^2}x - \sin x + C\). Câu 2 . Một vật chuyển động với vận tốc \(v(t) = 1,2 + \dfrac{{{t^2} + 4}}{{1 + 3}}\,\,\,(m/s)\). … [Đọc thêm...] vềĐề 10 – Kiểm Tra 1 tiết chương 3 giải tích 12
Kết quả tìm kiếm cho: ty so
Đề 8 – Kiểm Tra 1 tiết chương 3 giải tích 12
Đề bài Câu 1 . Tìm \(I = \int {{x^2}\cos x\,dx} \). A. \({x^2}.\sin x + x.\cos x - 2\sin x + C\). B. \({x^2}.\sin x + 2x.\cos x - 2\sin x + C\). C. \(x.\sin x + 2x.\cos x + C\). D. \(2x.\cos x + \sin + C\). Câu 2 . Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và \(y = \sqrt {x\sin x} \,\,(0 \le x \le … [Đọc thêm...] vềĐề 8 – Kiểm Tra 1 tiết chương 3 giải tích 12
Đề 6 – Kiểm Tra 1 tiết chương 3 giải tích 12
Đề bài Câu 1 . Cho hình (H) giới hạn bởi đường cong \({y^2} + x = 0\), trục Oy và hai đường thẳng y = 0, y= 1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính bởi: A. \(V = {\pi ^2}\int\limits_0^1 {{x^4}\,dx} \). B. \(V = \pi \int\limits_0^1 {{y^2}\,dy} \). C. \(V = \pi \int\limits_0^1 {{y^4}\,dy} \). D. \(V = \pi \int\limits_0^1 { - … [Đọc thêm...] vềĐề 6 – Kiểm Tra 1 tiết chương 3 giải tích 12
Bài 3: Ứng dụng của tích phân trong hình học
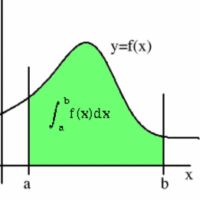
Thông qua bài học các bạn sẽ nắm được Ứng dụng của tích phân. Bên cạnh đó bài học còn giới thiệu đến các em ví dụ Ứng dụng của tích phân của một số hàm số cơ bản, các phần khác trong mục lục đầy đủ bên dưới. ============== Nội dung bài học: Lý thuyết Ứng dụng của tích phân trong hình học Ứng dụng tích phân tính diện tích hình phẳng Ứng … [Đọc thêm...] vềBài 3: Ứng dụng của tích phân trong hình học
Bài 1: Nguyên hàm – Giải tích 12
Thông qua bài học các bạn sẽ nắm được khái niệm, các tính chất của nguyên hàm . Bên cạnh đó bài học còn giới thiệu đến các em công thức tìm nguyên hàm của một số hàm số cơ bản, các phương pháp tìm nguyên hàm của một hàm số là phương pháp đổi biến số và phương pháp nguyên hàm từng phần và các phần khác trong mục lục đầy đủ bên dưới. ============== Nội dung … [Đọc thêm...] vềBài 1: Nguyên hàm – Giải tích 12
Sitemap
Sơ đồ website tại đây: CÁC BÀI VIẾT MỚI CHUYÊN MỤC DANH SÁCH TRANG MÂY THẺ … [Đọc thêm...] vềSitemap
Đề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word
Đề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word Cấu trúc đề minh họa kỳ thi THPT Quốc gia năm 2019 môn Toán: Chủ đề 1. Ứng dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số. 14 câu Chủ đề 2. Hàm số lũy thừa, hàm số mũ và hàm số logarit. 7 câu Chủ đề 3. Nguyên hàm, tích phân và ứng dụng. 5 câu Chủ đề 4. Số phức. 5 câu Chủ đề 5. … [Đọc thêm...] vềĐề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word
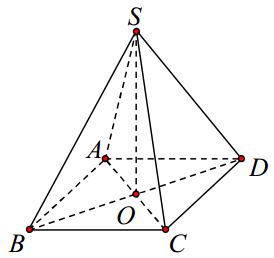
Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a, góc giữa cạnh bên hợp với mặt đáy bằng \({60^o}.\) Tính theo a thể tích khối chóp.
Câu hỏi: Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a, góc giữa cạnh bên hợp với mặt đáy bằng \({60^o}.\) Tính theo a thể tích khối chóp. A. \(V = \frac{{{a^3}\sqrt 3 }}{{12}}.\) B. \(V = \frac{{{a^3}}}{2}.\) C. \(V = \frac{{{a^3}\sqrt 3 }}{3}.\) D. \(V = \frac{{{a^3}\sqrt 3 }}{4}.\) trả lời câu hỏi trước khi xem đáp án bên dưới Đáp … [Đọc thêm...] vềCho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a, góc giữa cạnh bên hợp với mặt đáy bằng \({60^o}.\) Tính theo a thể tích khối chóp.
Lý thuyết thể tích của khối đa diện
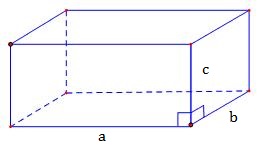
1. Tính chất của thể tích khối đa diện Hai khối đa diện bằng nhau thì có thể tích bằng nhau. Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ. Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1. 2. Thể tích khối hộp chữ nhật Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là … [Đọc thêm...] vềLý thuyết thể tích của khối đa diện
Tổng hợp kiến thức về 5 khối đa diện đều
Tổng hợp kiến thức cần nhớ về 5 khối đa diện đều, khối tứ diện đều, khối lập phương. khối bát diện đều, khối 12 mặt đều, khối 20 mặt đều. 1. Khối đa diện đều loại $\{3;3\}$ (khối tứ diện đều) • Mỗi mặt là một tam giác đều • Mỗi đỉnh là đỉnh chung của đúng 3 mặt • Có số đỉnh (Đ); số mặt (M); số cạnh (C) lần lượt là $D=4,M=4,C=6.$ • Diện tích tất cả các mặt của khối … [Đọc thêm...] vềTổng hợp kiến thức về 5 khối đa diện đều