Đề kiểm tra giữa kì 2 Toán 8 - Đề số 2 có lời giải chi tiết (4) Đề bài Câu 1 (2 điểm): Giải phương trình: a) \(\left( {3x - 2} \right)\left( {2x + 1} \right) = {\left( {2x + 1} \right)^2}\) b) \(\frac{2}{{x - 2}} - \frac{3}{{3 - x}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\) Câu 2 (2 điểm): Giải bài toán bằng cách lập … [Đọc thêm...] vềĐỀ THAM KHẢO THI GHK2 TOÁN LỚP 8 – ĐỀ 2
Kết quả tìm kiếm cho: ty so
ĐỀ THAM KHẢO THI GHK2 TOÁN LỚP 8 – ĐỀ 1
Đề kiểm tra giữa kì 2 Toán 8 - Đề số 1 có lời giải chi tiết (5) Đề bài Phần I: Trắc nghiệm (2,0 điểm) Ghi vào bài làm chữ cái đứng trước đáp án trả lời đúng ; a) Điều kiện xác định của phương trình \(\frac{x}{{3 - x}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}\) A. \(x \ne - 2\) hoặc \(x \ne 3\) B. \(x \ne 2\) và \(x \ne - 3\) … [Đọc thêm...] vềĐỀ THAM KHẢO THI GHK2 TOÁN LỚP 8 – ĐỀ 1
26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm \(S\), \({V_2}\) là thể tích khối còn lại. Tính \(\frac{{{V_1}}}{{{V_2}}}\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm … [Đọc thêm...] về26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm \(S\), \({V_2}\) là thể tích khối còn lại. Tính \(\frac{{{V_1}}}{{{V_2}}}\).
12. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). Biết \(AB = 4a\), \(AD = CD = 2a\). Cạnh bên \(SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(G\) là trọng tâm tam giác \(SBC\), \(M\) là điểm sao cho \(\overrightarrow {MA} = – 2\overrightarrow {MS} \) và \(E\) là trung điểm cạnh \(CD\) ( tham khảo hình vẽ). Tính thể tích \(V\) của khối đa diện \(MGABE\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 12. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). Biết \(AB = 4a\), \(AD = CD = 2a\). Cạnh bên \(SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(G\) là trọng tâm tam giác \(SBC\), \(M\) là điểm sao cho … [Đọc thêm...] về12. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). Biết \(AB = 4a\), \(AD = CD = 2a\). Cạnh bên \(SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(G\) là trọng tâm tam giác \(SBC\), \(M\) là điểm sao cho \(\overrightarrow {MA} = – 2\overrightarrow {MS} \) và \(E\) là trung điểm cạnh \(CD\) ( tham khảo hình vẽ). Tính thể tích \(V\) của khối đa diện \(MGABE\).
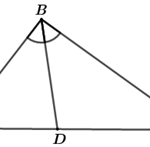
6. Cho hình chóp \(S.ABC\), tam giác \(ABC\) cân tại \(B\), \(AC = a\sqrt 3 ,\,\,\widehat {ABC} = 120^\circ \), tam giác \(SBC\) cân tại \(S\), \(SB\) vuông góc \(AC\), góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính \(\sin \) của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 6. Cho hình chóp \(S.ABC\), tam giác \(ABC\) cân tại \(B\), \(AC = a\sqrt 3 ,\,\,\widehat {ABC} = 120^\circ \), tam giác \(SBC\) cân tại \(S\), \(SB\) vuông góc \(AC\), góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ \). … [Đọc thêm...] về6. Cho hình chóp \(S.ABC\), tam giác \(ABC\) cân tại \(B\), \(AC = a\sqrt 3 ,\,\,\widehat {ABC} = 120^\circ \), tam giác \(SBC\) cân tại \(S\), \(SB\) vuông góc \(AC\), góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính \(\sin \) của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\).
11. Cho hình chóp \(S.ABCD\) có thể tích bằng \(36{a^3}\sqrt 2 \), \(AB = 6a,\) tam giác \(SAB\) đều, tứ giác \(ABCD\) là hình bình hành. Gọi \(I\) là điểm thuộc đường thẳng \(SB\) sao cho \(\overrightarrow {SI} = \frac{2}{5}\overrightarrow {SB} \), \(E\) là điểm thuộc đường thẳng \(SC\)sao cho \(\overrightarrow {SE} = \frac{2}{3}\overrightarrow {SC} \), gọi \(H\) là trọng tâm tam giác \(ACD\). Tính khoảng cách giữa hai đường thẳng \(AI\) và \(HE\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 11. Cho hình chóp \(S.ABCD\) có thể tích bằng \(36{a^3}\sqrt 2 \), \(AB = 6a,\) tam giác \(SAB\) đều, tứ giác \(ABCD\) là hình bình hành. Gọi \(I\) là điểm thuộc đường thẳng \(SB\) sao cho \(\overrightarrow {SI} = \frac{2}{5}\overrightarrow {SB} \), … [Đọc thêm...] về11. Cho hình chóp \(S.ABCD\) có thể tích bằng \(36{a^3}\sqrt 2 \), \(AB = 6a,\) tam giác \(SAB\) đều, tứ giác \(ABCD\) là hình bình hành. Gọi \(I\) là điểm thuộc đường thẳng \(SB\) sao cho \(\overrightarrow {SI} = \frac{2}{5}\overrightarrow {SB} \), \(E\) là điểm thuộc đường thẳng \(SC\)sao cho \(\overrightarrow {SE} = \frac{2}{3}\overrightarrow {SC} \), gọi \(H\) là trọng tâm tam giác \(ACD\). Tính khoảng cách giữa hai đường thẳng \(AI\) và \(HE\).
19. Cho tứ diện \(ABCD\) có \(AB = a,CD = 2a\), góc giữa hai đường thẳng \(AD\) và \(BC\)bằng \(60^\circ \), \(\Delta ABD\) vuông tại \(A\); \(\Delta ABC\) vuông tại \(B\). Khi thể tích khối tứ diện \(ABCD\) lớn nhất, tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 19. Cho tứ diện \(ABCD\) có \(AB = a,CD = 2a\), góc giữa hai đường thẳng \(AD\) và \(BC\)bằng \(60^\circ \), \(\Delta ABD\) vuông tại \(A\); \(\Delta ABC\) vuông tại \(B\). Khi thể tích khối tứ diện \(ABCD\) lớn nhất, tính khoảng cách giữa hai đường thẳng … [Đọc thêm...] về19. Cho tứ diện \(ABCD\) có \(AB = a,CD = 2a\), góc giữa hai đường thẳng \(AD\) và \(BC\)bằng \(60^\circ \), \(\Delta ABD\) vuông tại \(A\); \(\Delta ABC\) vuông tại \(B\). Khi thể tích khối tứ diện \(ABCD\) lớn nhất, tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD\).
31. Cho lăng trụ tứ giác đều \(ABCD.A’B’C’D’\) có cạnh bên bằng \(2a\), cạnh đáy bằng \(a\). Gọi \(I\) là trung điểm của \(DD’\). Tính cosin của góc giữa hai mặt phẳng \(\left( {IAC} \right)\) và \(\left( {ACC’A’} \right)\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 31. Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có cạnh bên bằng \(2a\), cạnh đáy bằng \(a\). Gọi \(I\) là trung điểm của \(DD'\). Tính cosin của góc giữa hai mặt phẳng \(\left( {IAC} \right)\) và \(\left( {ACC'A'} \right)\). A. \(\frac{{\sqrt 6 … [Đọc thêm...] về31. Cho lăng trụ tứ giác đều \(ABCD.A’B’C’D’\) có cạnh bên bằng \(2a\), cạnh đáy bằng \(a\). Gọi \(I\) là trung điểm của \(DD’\). Tính cosin của góc giữa hai mặt phẳng \(\left( {IAC} \right)\) và \(\left( {ACC’A’} \right)\).
38. Cho lăng trụ đứng \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A\). Khoảng cách giữa đường thẳng \(AA’\) với mặt phẳng \(BCC’B’\) bằng khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {ABC’} \right)\) và cùng bằng \(x\). Góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABC’} \right)\) bằng \(\alpha \). Tính \(\tan \alpha \) khi thể tích khối lăng trụ \(ABC.A’B’C’\) nhỏ nhất.
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 38. Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\). Khoảng cách giữa đường thẳng \(AA'\) với mặt phẳng \(BCC'B'\) bằng khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {ABC'} \right)\) và cùng bằng \(x\). Góc giữa hai mặt phẳng … [Đọc thêm...] về38. Cho lăng trụ đứng \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A\). Khoảng cách giữa đường thẳng \(AA’\) với mặt phẳng \(BCC’B’\) bằng khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {ABC’} \right)\) và cùng bằng \(x\). Góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABC’} \right)\) bằng \(\alpha \). Tính \(\tan \alpha \) khi thể tích khối lăng trụ \(ABC.A’B’C’\) nhỏ nhất.
29. Cho hình lăng trụ \(ABCD.A’B’C’D’\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B’\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB’\) là tam giác vuông cân. Gọi \(\alpha \) là góc giữa hai đường thẳng \(BH\) và \(AC’\). Khi đó, \(\cos \alpha \) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 29. Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B'\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB'\) là tam giác vuông cân. Gọi … [Đọc thêm...] về29. Cho hình lăng trụ \(ABCD.A’B’C’D’\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B’\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB’\) là tam giác vuông cân. Gọi \(\alpha \) là góc giữa hai đường thẳng \(BH\) và \(AC’\). Khi đó, \(\cos \alpha \) bằng