Một viên đạn được bắn thẳng đứng lên trên từ độ cao $2\text{m}$ với vận tốc tại thời điểm $t$ cho bởi công thức $v\left( t \right)=100-9,8t\left( \text{m/s} \right)$, ( $t=0$ là thời điểm viên đạn được bắn lên). Tìm độ cao (tính theo $\text{km}$ ) của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất (làm tròn đến hàng phần trăm).
Lời giải
Đáp án: $0,51$.
Gọi $h\left( t \right)$ là độ cao (tính bằng mét) của viên đạn tại thời điểm $t$ (tính bằng giây).
Ta có: $h\left( t \right)=\int{v\left( t \right)\text{d}t=\int{\left( 100-9,8t \right)\text{d}t=-4,9{{t}^{2}}+100t+C}}$.
Tại thời điểm $t=0$, ta có $h\left( t \right)=2\Rightarrow C=2$.
Vậy $h\left( t \right)=-4,9{{t}^{2}}+100t+2$.
${h}’\left( t \right)=-9,8t+100;$
${h}’\left( t \right)=0\Leftrightarrow t=\dfrac{500}{49}$.
BBT:
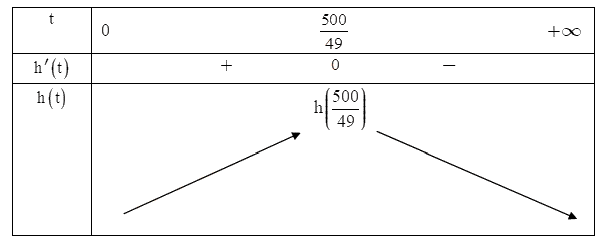
Từ bảng biến thiên suy ra viên đạn đạt độ cao lớn nhất tại thời điểm $t=\dfrac{500}{49}$.
Do đó độ cao của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất là $h\left( \dfrac{500}{49}+1 \right)\approx 507,3\text{m}\approx 0,51\text{km}$.
