Một vật chuyển động với hàm số gia tốc là $a\left( t \right)$. Biết rằng đồ thị hàm số $a\left( t \right)$ trên đoạn $\left[ 0;6 \right]$ được cho như hình dưới đây và vận tốc tại thời điểm $t=0$ là $v\left( 0 \right)=1\ \left( m/s \right)$.
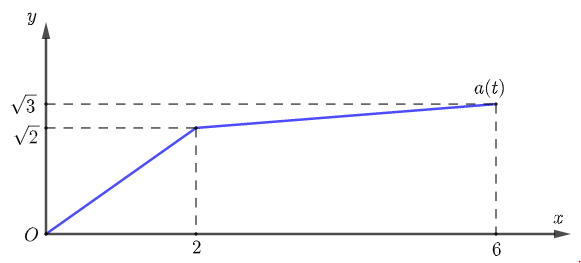
Tại thời điểm $t=6$ giây, vận tốc của vật là bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải
Trả lời: 8,7
Từ đồ thị ta có $a\left( t \right)=\left\{ \begin{array}{l}
\dfrac{\sqrt{2}}{2}t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,0\le t\le 2 \\
\dfrac{\sqrt{3}-\sqrt{2}}{4}t+\dfrac{3\sqrt{2}-\sqrt{3}}{2}\ \ \ \ ,\ 2\le t\le 6\ \ \\
\end{array} \right.$.
Mà $v\left( 0 \right)=1\ \left( m/s \right)$ nên $v\left( t \right)=\int{a\left( t \right)\text{d}t}=\left\{ \begin{array}{l}
\dfrac{\sqrt{2}}{4}{{t}^{2}}+1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,0\le t\le 2 \\
\dfrac{\sqrt{3}-\sqrt{2}}{8}{{t}^{2}}+\dfrac{3\sqrt{2}-\sqrt{3}}{2}t+C\ \ ,2\le t\le 6 \\
\end{array} \right.$.
Vì vận tốc là hàm số liên tục nên
$\lim\limits_{t\to {{2}^{-}}} v\left( t \right)=\lim\limits_{x\to {{2}^{+}}} v\left( t \right)\Leftrightarrow \sqrt{2}+1=\dfrac{\sqrt{3}-\sqrt{2}}{2}+3\sqrt{2}-\sqrt{3}+C\Leftrightarrow C=\dfrac{\sqrt{3}-3\sqrt{2}+2}{2}$.
Do đó $v\left( 6 \right)=1+3\sqrt{2}+2\sqrt{3}\ \approx 8,7\left( m/s \right)$.
