A. \(10.250.000\) đồng.
B. \(13.525.000\) đồng.
C. \(18.450.000\) đồng.
D. \(16.230.000\) đồng.
Lời giải:
Đặt hệ trục tọa độ như hình vẽ, khi đó phương trình đường parabol có dạng: \(y = a{x^2} + b\).
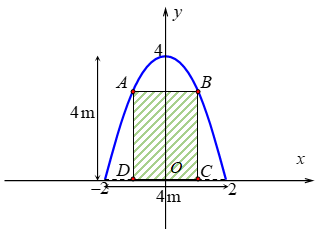
Parabol cắt trục tung tại điểm \(\left( {0;4} \right)\) và cắt trục hoành tại \(\left( {2;0} \right)\) nên:
\(\left\{ \begin{array}{l}b = 4\\a{.2^2} + b = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = – 1\\b = 4\end{array} \right.\).
Do đó, phương trình parabol là \(y = – {x^2} + 4\).
Diện tích hình phẳng giới hạn bởi đường parabol và trục hoành là
\({S_1} = \int\limits_{ – 2}^2 {\left( { – {x^2} + 4} \right){\mathop{\rm d}\nolimits} x} \)\( = \left. {\left( { – \frac{{{x^3}}}{3} + 4x} \right)} \right|_{ – 2}^2\)\( = \frac{{32}}{3}\).
Gọi \(C\left( {t;0} \right)\) \( \Rightarrow B\left( {t;4 – {t^2}} \right)\) với \(0 < t < 2\).
Ta có \(CD = 2t\) và \(BC = 4 – {t^2}\). Diện tích hình chữ nhật \(ABCD\) là
\({S_2} = CD.BC\) \( = 2t.\left( {4 – {t^2}} \right)\)\( = – 2{t^3} + 8t\).
Diện tích phần trang trí hoa văn là
\(S = {S_1} – {S_2}\)\( = \frac{{32}}{3} – \left( { – 2{t^3} + 8t} \right)\)\( = 2{t^3} – 8t + \frac{{32}}{3}\).
Xét hàm số \(f\left( t \right) = 2{t^3} – 8t + \frac{{32}}{3}\) với \(0 < t < 2\).
Ta có \(f’\left( t \right) = 6{t^2} – 8 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = \frac{2}{{\sqrt 3 }} \in \left( {0;2} \right)\\t = – \frac{2}{{\sqrt 3 }} \notin \left( {0;2} \right)\end{array} \right.\).
Suy ra diện tích phần trang trí nhỏ nhất là bằng \(\frac{{96 – 32\sqrt 3 }}{9}{{\mathop{\rm m}\nolimits} ^2}\), khi \(t = \frac{2}{{\sqrt 3 }}\). Khi đó, chi phí thấp nhất cho việc hoàn tất hoa văn trên cổng nhà sẽ là \(\frac{{96 – 32\sqrt 3 }}{9}.3000000 \approx 13525000\) đồng.
=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ NGUYÊN HAM – TICH PHÂN – ỨNG DỤNG.