1. Các kiến thức cần nhớ
Định nghĩa:
– Hàm số lũy thừa là hàm số có dạng \(y = {x^\alpha }\left( {\alpha \in R} \right)\).
– Tập xác định:
+ \(\alpha \) nguyên dương: \(D = R\).
+ \(\alpha \) nguyên âm hoặc \(\alpha = 0\): \(D = R\backslash \left\{ 0 \right\}\).
+ \(\alpha \) không nguyên: \(D = \left( {0; + \infty } \right)\).
Chú ý:
Đạo hàm:
\(\left( {{x^\alpha }} \right)’ = \alpha {x^{\alpha – 1}};{u^\alpha }\left( x \right)’ = \alpha u’\left( x \right){u^{\alpha – 1}}\left( x \right)\)
\(\left( {\sqrt[n]{x}} \right)’ = \dfrac{1}{{n\sqrt[n]{{{x^{n – 1}}}}}};\left( {\sqrt[n]{{u\left( x \right)}}} \right)’ = \dfrac{{u’\left( x \right)}}{{n\sqrt[n]{{{u^{n – 1}}\left( x \right)}}}}\)
+ Nếu \(x \le 0\) thì đẳng thức trên không xảy ra.
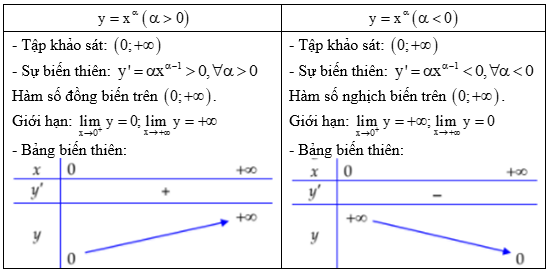
Khảo sát hàm số \(y = {x^\alpha }\left( {\alpha \ne 0} \right)\) trên tập \(\left( {0; + \infty } \right)\).

– Đồ thị:
Luôn đi qua điểm \(\left( {1;1} \right)\)
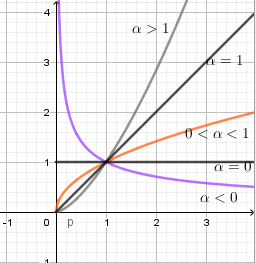
– Trên đây ta chỉ xét chung các hàm số trên tập \(\left( {0; + \infty } \right)\). Thực tế tập xác định của mỗi hàm số là khác nhau phụ thuộc vào điều kiện của \(\alpha \).
– Tránh nhầm lẫn tập \(\left( {0; + \infty } \right)\) là tập xác định cho mọi hàm số lũy thừa.
2. Một số dạng toán thường gặp
Dạng 1: Tìm tập xác định của hàm số.
Phương pháp:
– Bước 1: Xác định số mũ \(\alpha \) của hàm số.
– Bước 2: Nêu điều kiện để hàm số xác định.
+ \(\alpha \) nguyên dương: \(D = R\).
+ \(\alpha \) nguyên âm hoặc \(\alpha = 0\): \(D = R\backslash \left\{ 0 \right\}\).
+ \(\alpha \) không nguyên: \(D = \left( {0; + \infty } \right)\).
– Bước 3: Giải các bất phương trình ở trên để tìm tập xác định của hàm số.
Dạng 2: Tính đạo hàm của hàm số.
Phương pháp:
– Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
\(\left( {u \pm v} \right)’ = u’ \pm v’;\left( {uv} \right)’ = u’v + uv’;\left( {\dfrac{u}{v}} \right)’ = \dfrac{{u’v – uv’}}{{{v^2}}}\)
– Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
– Bước 3: Tính toán và kết luận.
Dạng 3: Tìm mỗi quan hệ của các số mũ của các hàm số lũy thừa khi biết đồ thị của chúng.
Phương pháp:
Quan sát đồ thị hàm số và nhận xét tính đồng biến, nghịch biến và các điểm đi qua để suy ra tính chất của các số mũ.
===========
3. Bài tập minh họa
Ví dụ 1:
Tìm tập xác định của các hàm số sau:
a) \(y=x^6\)
b) \(y=(1-x)^{\sqrt2}\)
c) \(y=(x+2)^{-3}\)
Lời giải:
a) Hàm số \(y=x^6\) xác định với mọi \(x\in\mathbb{R}\).
Vậy tập xác định của hàm số là \(D=\mathbb{R}.\)
b) Hàm số \(y=(1-x)^{\sqrt2}\) xác định khi \(1 – x > 0 \Leftrightarrow x < 1.\)
Vậy tập xác định của hàm số là \(D = \left( { – \infty ;1} \right)\).
c) Hàm số \(y=(x+2)^{-3}\) xác định khi \(x + 2 \ne 0 \Leftrightarrow x \ne – 2\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { – 2} \right\}.\)
Ví dụ 2:
Tính đạo hàm các hàm số
a) \(y = {x^{\sqrt 2 + 1}}\)
b) \(y = {x^{3\pi }}\)
c) \(y=x^{-0,9}\)
Lời giải:
a) \(y’ = – \frac{1}{2}{x^{ – \frac{1}{2} – 1}} = – \frac{1}{2}{x^{ – \frac{3}{2}}} = – \frac{1}{{2\sqrt {{x^3}} }}.\)
b) \(y’ = 3\pi .{x^{3\pi – 1}}\).
c) \(y’ = – 0,9{x^{ – 0,9 – 1}} = – 0,9{x^{ – 1,9}}.\)
Ví dụ 3:
Tính đạo hàm các hàm số sau:
a) \(y = {(2x + 1)^\pi }\)
b) \(y = {(3{x^2} – 1)^{ – \sqrt 2 }}\)
c) \(y = {\left( {2{x^2} + x – 1} \right)^{\frac{2}{3}}}\)
Lời giải:
a) \(y’ = \pi {(2x + 1)^{\pi – 1}}(2x + 1)’ = 2\pi {(2x + 1)^{\pi – 1}}.\)
b) \(y’ = – \sqrt 2 {\left( {3{x^2} – 1} \right)^{ – \sqrt 2 – 1}}(3{x^2} – 1)’ = – 6\sqrt 2 x{(3{x^2} – 1)^{ – \sqrt 2 – 1}}.\)
c) \(y’ = \frac{2}{3}{(2{x^2} + x – 1)^{ – \frac{1}{3}}}(4x + 1).\)
=====
XEM TRẮC NGHIỆM
https://booktoan.com/trac-nghiem-ham-so-luy-thua-va-ham-so-mu
=======
