Đề: Xét hàm số với tham số a:                                       \(y = \frac{{{x^2} + 3x + a}}{{x + 1}}\)1. Với những giá trị nào của tham số $a$ thì đồ thị của hàm số trên có tiếp tuyến vuông góc với đường phân giác của góc phần tư thứ nhất của hệ trục tọa độ?. Chứng minh rằng khi đó đồ thị của hàm số có điểm cực đại và điểm cực tiểu.2. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $a = 3.$

Đề bài: Xét hàm số với tham số a:                                       \(y = \frac{{{x^2} + 3x + a}}{{x + 1}}\)1. Với những giá trị nào của tham số $a$ thì đồ thị của hàm số trên có tiếp tuyến vuông góc với đường phân giác của góc phần tư thứ nhất của hệ trục tọa độ?. Chứng minh rằng khi đó đồ thị của hàm số có điểm cực đại và điểm cực tiểu.2. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $a = 3.$

Lời giải

$1.$ \(y’ = \frac{{{x^2} + 2x + 3 – a}}{{{{\left( {x + 1} \right)}^2}}}\). Đồ thị có tiếp tuyến vuông góc với đường phân giác góc phần tư thứ nhất
$\Leftrightarrow$  phương trình  \(\frac{{{{(x + 1)}^2} + 2 – a}}{{{{(x + 1)}^2}}} =  – 1\) có nghiệm
$\Leftrightarrow$ phương trình  \(2{\left( {x + 1} \right)^2} = a – 2\) có nghiệm  \(x \ne  – 1 \Leftrightarrow a – 2 > 0 \Leftrightarrow a > 2\).
Với $a > 2$ thì tam thức  \({x^2} + 2x + 3 – a\) có \(\Delta ‘ = a – 2 > 0 \Rightarrow y’\) có $2$ nghiệm phân biệt$\Rightarrow$ Hàm số có \({y_{C{\rm{D}},}}{y_{CT}}\)
$2.$ Với $a=3$, ta có phương trình hàm số: $y=\frac{x^2+3x+3}{x+1}$
1. TẬP XÁC ĐỊNH: $D = (-\infty ; -1) \cup (-1 ; +\infty)$
2. SỰ BIẾN THIÊN
    a) Đạo hàm
$        y’ = 1-\frac1{(x+1)^2}$
$        y’ = 0 \Leftrightarrow x = -2 \vee x = 0 ; $
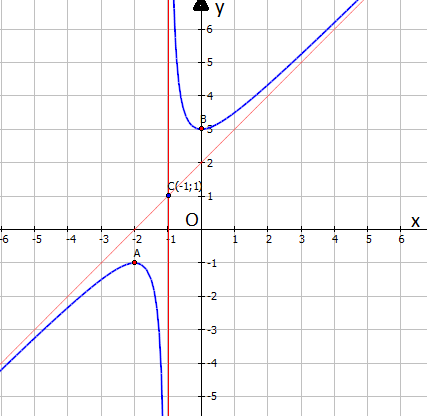
Hàm số đạt 2 cực trị tại: $A ( -2 ; -1 ), B ( 0 ; 3 )$
    b) Giới hạn và các đường tiệm cận
        + Ta có: $\mathop {\lim y}\limits_{x \to -1^-}=-\infty$; $\mathop {\lim y}\limits_{x \to -1^+}=+\infty$
Suy ra đường thẳng $x = -1$ là tiệm cận đứng của đồ thị hàm số đã cho
        + Giới hạn tại vô cực: $\mathop {\lim y}\limits_{x \to +\infty}=+\infty; \mathop {\lim y}\limits_{x \to -\infty}=-\infty$
        + Ta có: $\mathop {\lim (y-(x+2))}\limits_{x \to +\infty}=0;  \mathop {\lim (y-(x+2))}\limits_{x \to -\infty}=0$
Suy ra:  đường thẳng $y = x+2$ là tiệm cận xiên của đồ thị hàm số đã cho
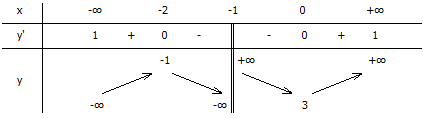
    c) Bảng biến thiên

 d) Chiều biến thiên và các cực trị
        + Hàm số đồng biến trên $( -\infty ; -2 )$
        + Hàm số nghịch biến trên $( -2 ; -1 )$
        + Hàm số nghịch biến trên $( -1 ; 0 )$
        + Hàm số đồng biến trên $( 0 ; +\infty )$
        + Hàm số đạt cực đại tại điểm $x = -2$; giá trị cực đại của hàm số là $y = -1$
        + Hàm số đạt cực tiểu tại điểm $x = 0$; giá trị cực tiểu của hàm số là $y = 3$
3. ĐỒ THỊ
    a) Giao điểm của đồ thị với các trục tọa độ
        + Giao điểm của hàm số với trục $Ox$:             $y = 0$ Vô nghiệm, hàm số không cắt trục $Ox$
        + Giao điểm của hàm số với trục $Oy$:            $ x = 0 \Leftrightarrow y = 3$
    b) Nhận xét
        + Đồ thị hàm số nhận giao điểm $C (-1;1)$ của $2$ tiệm cận làm tâm đối xứng
    c) Vẽ đồ thị hàm số