Câu hỏi:
Cho hình tròn bán kính R=2. Người ta cắt bỏ đi \(\frac{1}{4}\) hình tròn rồi dùng phần còn lại để dán lại tạo nên một mặt xung quanh của hình nón (H). Tính diện tích toàn phần S của hình nón (H).
- A. \(S = 3\pi .\)
- B. \(S = \left( {3 + 4\sqrt 3 } \right)\pi .\)
- C. \(S = \left( {3 + 3\sqrt 2 } \right)\pi .\)
- D. \(S = \frac{{21\pi }}{4}.\)
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: D
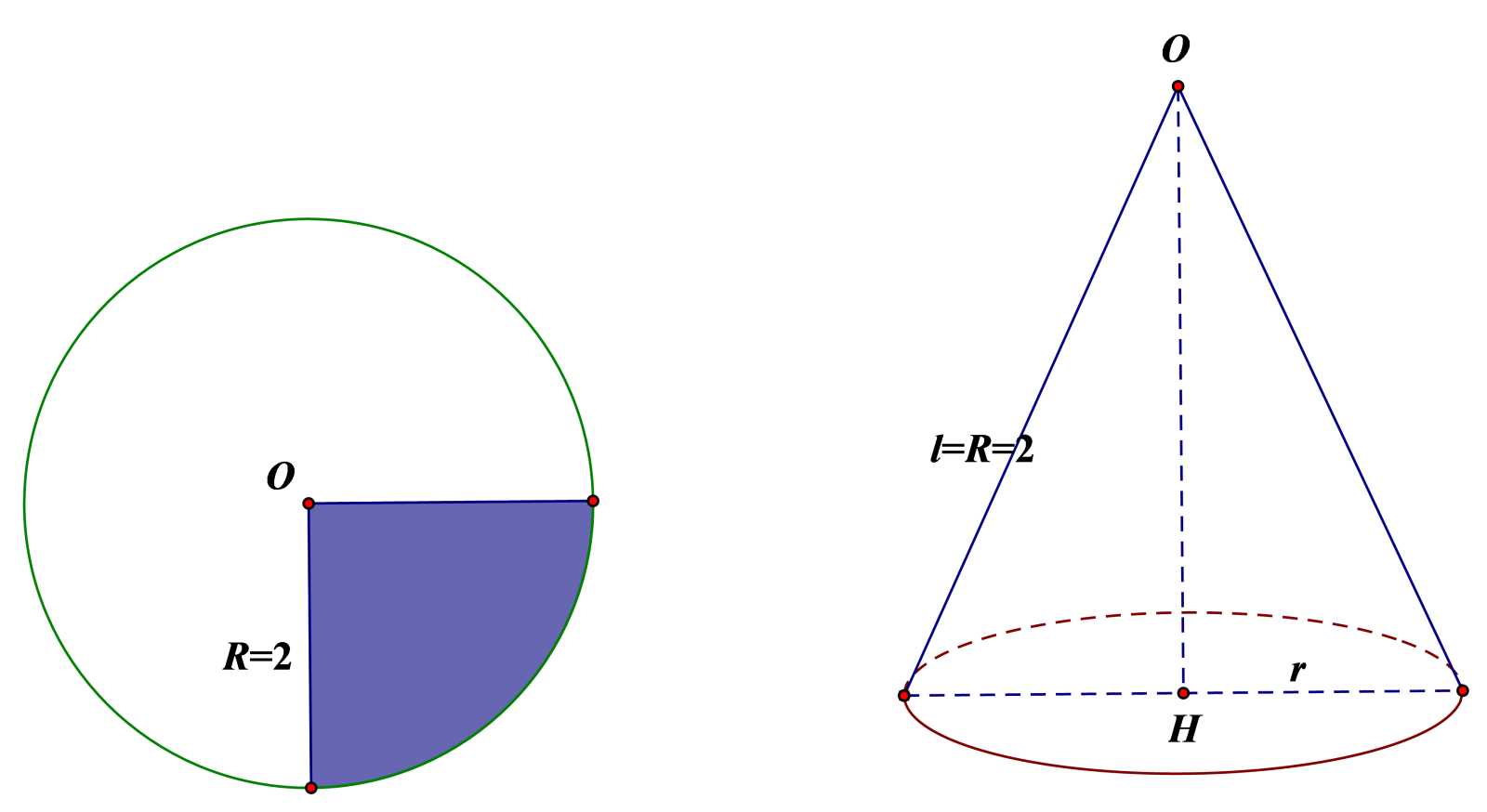
Chu vi của đường tròn đáy nón bằng \(\frac{3}{4}\) chu vi của đường tròn ban đầu nên chu vi của đường tròn đáy nón bằng \(3\pi.\)
Bán kính của đường tròn đáy nón là \(r=\frac{3}{2}.\).
Đường sinh của nón bằng bán kính của đường tròn ban đầu.
Vậy diện tích toàn phần khối nón là \({S_{tp}} = l\pi r + \pi {r^2} = 2\pi .\frac{3}{2} + \pi {\left( {\frac{3}{2}} \right)^2} = \frac{{21}}{4}\pi .\)
=======
Xem thêm Lý thuyết khối tròn xoay
Bài học cùng chương bài
- Đề: Một các nón lá có bán kính đáy là 20cm và đường sinh là 30cm. Tính diện tích xung quanh của cái nón.
- Đề: Tính diện tích xung quanh \({S_{xq}}\) của hình nón có bán kính đáy là đường sinh có độ dài lần lượt là 3cm và 12cm.
- Đề: Cho hình nón có chiều cao bằng đường kính đáy và bằng 2. Tính diện tích xung quanh của hình nón đó.
- Đề: Một hình nón đỉnh S, đáy hình tròn tâm O và \(SO = h.\) Một mặt phẳng (P) qua đỉnh S cắt đường tròn (O) theo dây cung AB sao cho \(\widehat {AOB} = {90^o},\) biết khoảng cách từ O đến (P) bằng \(\frac{h}{2}.\) Khi đó diện tích xung quanh của hình nón bằng:
- Đề: Trong không gian, cho tam giác \(OAB\) vuông tại \(O\) có \(OA = 4a\), \(OB = 3a\). Nếu cho tam giác \(OAB\) quay quanh cạnh \(OA\) thì mặt nón tạo thành có diện tích xung quanh \({S_{xq}}\) bằng bao nhiêu?
- Đề: Một hình trụ có hai đáy là hai hình tròn \(\left( {O;R} \right)\) và \(\left( {O';R} \right),OO' = R\sqrt 3 .\) Một hình nón có đỉnh là O’ và đáy là hình tròn \(\left( {O;R} \right).\) Gọi \({S_1},{S_2}\) lần lượt là diện tích xung quanh của hình trụ và hình nón. Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}.\)
- Đề: Hình nón có chiều cao \(10\sqrt 3 cm,\) góc giữa một đường sinh với mặt đáy bằng \({60^0}.\) Tính diện tích xung quanh S của hình nón.
- Đề: Cho đoạn thẳng AB có độ dài bằng 2a, vẽ tia Ax về phía điểm B sao cho điểm B luôn cách tia Ax một đoạn bằng a. Gọi H là hình chiếu của B lên tia Ax, khi tam giác AHB quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có diện tích xung quanh bằng bao nhiêu?
- Đề: Cho tam giác ABC vuông tại A có AB=6, AC=8. Tính diện tích xung quanh của hình nón tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AC.
- Đề: Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. Tính diện tích xung quanh S của hình nón.
- Đề: Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng 2. Tính diện tích xung quanh của hình nón.
- Đề: Cho hình nón có độ dài đường sinh bằng 2 cm, góc ở đỉnh bằng 600. Tìm S là diện tích xung quanh của hình nón.
- Đề: Cho khối nón đỉnh O trục OI, bán kính đáy bằng a và chiều cao bằng \(\frac{a}{2}\). Mặt phẳng (P) thay đổi luôn 2 luôn đi qua O và cắt hình nón theo thiết diện là tam giác ABO. Tìm S là diện tích lớn nhất của tam giác ABO.
- Đề: Cho tam giác ABO vuông tại O, có góc \(\widehat {BAO} = {30^0},AB = a\). Quay tam giác ABO quanh trục AO ta được một hình nón. Tính diện tích xung quanh hình nón đó.
- Đề: Cho hình lập phương ABCD.A’B’C’D’ có cạnh b. Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra khi quay tam giác AA’C’ quanh trục AA’. Tính S.
Trả lời