Đề: Cho hàm số:$y = \frac{{{{\left( {x + 1} \right)}^2}}}{{x + 2}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Biện luận theo tham số $m$ về nghiệm của phương trình sau:${\left( {x + 1} \right)^2} – m.\left| {x + 2} \right| = 0$

Đề bài: Cho hàm số:$y = \frac{{{{\left( {x + 1} \right)}^2}}}{{x + 2}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Biện luận theo tham số $m$ về nghiệm của phương trình sau:${\left( {x + 1} \right)^2} – m.\left| {x + 2} \right| = 0$

Lời giải

$1.$ Xin dành cho bạn đọc. 
$2)$ Phương trình đã cho có thể viết lại thành: $m = \frac{{{{\left( {x + 1} \right)}^2}}}{{|x + 2|}}$
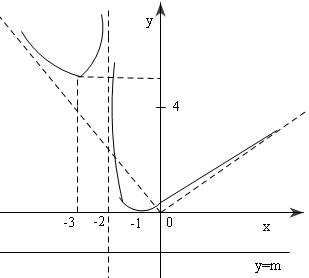
Số nghiệm của phương trình là số giao điểm của đường thẳng $y = m$ với đồ thị $y = f(x) =\frac{{{{\left( {x + 1}\right)}^2}}}{{|x + 2|}}$
Vì $f(x) =\left\{ \begin{array}{l}\frac{{{{\left( {x + 1} \right)}^2}}}{{x + 2}}\,\,\,\,\,;\,\,x >  – 2\\
 – \frac{{{{\left( {x + 1} \right)}^2}}}{{x + 2}}\,\,\,;\,\,x \end{array} \right.$ nên đồ thị y = f(x) trùng với đồ thị đã vẽ ở phần $1)$ ứng với $x> -2$; đối xưng
với đồ thị đã vẽ ở phần $1)$ qua trục hoành (ứng với $x Từ đồ thị rút ra kết luận sau:
+ Nếu $m + Nếu $m = 0$ thì pt có nghiệm duy nhất.
+ Nếu $0 + Nếu $m = 4$ thì phương trình có $3$ nghiệm phân biệt.
+ Nếu $m > 4$ thì pt có $4$ nghiệm phân biệt.