
Câu hỏi:
Cho mặt cầu \(\left( S \right)\) có bán kính R. Một hình nón \(\left( N \right)\) có chiều cao \(x\left( {0 < x < 2R} \right)\) nội tiếp trong hình cầu \(\left( S \right).\) Gọi \({V_S},{V_N}\) lần lượt là thể tích của khối cầu \(\left( S \right)\) và khối nón \(\left( N \right).\) Giá trị lớn nhất của tỉ số \(\frac{{{V_N}}}{{{V_S}}}\) bằng bao nhiêu?
- A. \(\frac{1}{3}.\)
- B. \(\frac{8}{{27}}.\)
- C. \(\frac{9}{{32}}.\)
- D. \(\frac{1}{4}.\)
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: B
Mặt phẳng thiết diện vuông góc với đáy của hình nón và đi qua đường cao của hình nón như hình vẽ bên.
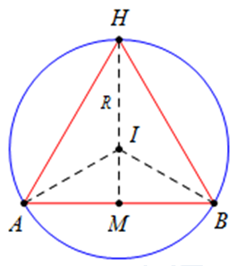
Chuẩn hóa \(R = 1,HM = x\) là chiều cao của khối nón
Tam giác IMA vuông tại M, có \(AM = \sqrt {I{A^2} – I{M^2}} = \sqrt {2{\rm{x}} – {x^2}} .\)
Khối nón (N) có chiều cao \(h = x,\) bán kính đáy \(r = AM = \sqrt {2x – {x^2}} .\)
\( \Rightarrow {V_N} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \left( {2{\rm{x}} – {x^2}} \right)x = \frac{1}{3}\pi {{\rm{x}}^2}\left( {2 – x} \right) = \frac{4}{3}\pi .\frac{x}{2}.\frac{x}{2}.\left( {2 – x} \right)\)
\(\,\,\,\,\, \le \frac{4}{3}\pi .\frac{{{{\left( {\frac{x}{2} + \frac{x}{2} + 2 – x} \right)}^3}}}{{27}} = \frac{4}{3}\pi .\frac{{{2^3}}}{{27}} = \frac{{32}}{{81}} \Rightarrow \frac{{{V_N}}}{{{V_S}}} = \frac{{32}}{{81}}\pi :\left( {\frac{4}{3}\pi } \right) = \frac{8}{{27}}.\)
=======
Xem thêm Lý thuyết khối tròn xoay
