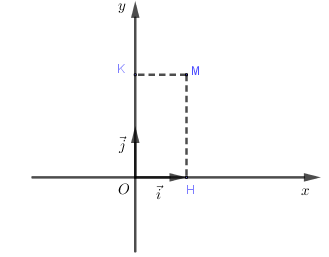
1. Định nghĩa Hệ trục tọa độ gồm hai trục vuông góc \(Ox\) và \(Oy\) với hai vectơ đơn vị lần lượt là \(\overrightarrow i ,\,\overrightarrow j \). Điểm O gọi là gốc tọa độ, \(Ox\) gọi là trục hoành và \(Oy\) gọi là trục tung. Kí hiệu \(Oxy\) hay \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\) 2. Tọa độ điểm, tọa độ vec tơ + Trong hệ trục tọa độ … [Đọc thêm...] vềBài 4. Hệ trục tọa độ – Chương 1 – Hình học 10
Bài 3. Tích của vectơ với một số – Chương 1 – Hình học 10
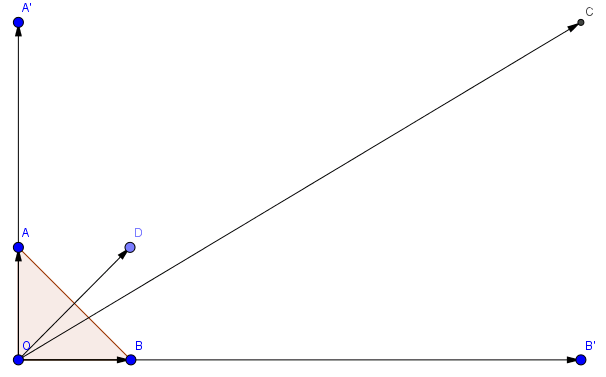
1. Định nghĩa Tích của vectơ $\overrightarrow a $ với số thực \(k \ne 0\) là một vectơ, kí hiệu là $k\overrightarrow a $, cùng hướng với $\overrightarrow a $ nếu $k > 0$, ngược hướng với $\overrightarrow a $ nếu $k < 0$ và có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) Quy ước: $0\overrightarrow a = \overrightarrow 0 $ và $k\overrightarrow 0 … [Đọc thêm...] vềBài 3. Tích của vectơ với một số – Chương 1 – Hình học 10
Bài 2. Tổng và hiệu của hai vectơ – Chương 1 – Hình học 10
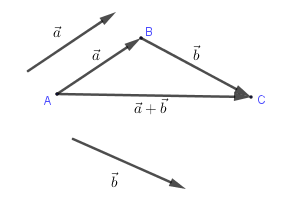
1. Tổng hai vectơ a) Định nghĩa Cho hai vectơ $\overrightarrow a \,;\,\,\overrightarrow b $. Từ điểm A tùy ý vẽ $\overrightarrow {AB} = \overrightarrow a $ rồi từ B vẽ $\overrightarrow {BC} = \overrightarrow b $. Khi đó vectơ $\overrightarrow {AC} $ được gọi là tổng của hai vectơ $\overrightarrow a \,;\,\,\overrightarrow b $. Kí hiệu $\overrightarrow {AC} = … [Đọc thêm...] vềBài 2. Tổng và hiệu của hai vectơ – Chương 1 – Hình học 10
Bài 1. Các định nghĩa Vecto – Chương 1 – Hình học 10
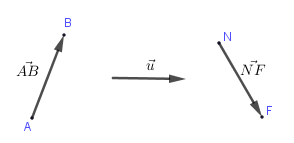
1. Định nghĩa vectơ Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối. Vectơ có điểm đầu là $A,$ điểm cuối là $B$ ta kí hiệu $\overrightarrow {AB} $ Vectơ còn được kí hiệu là: $\overrightarrow a ,{\rm{ }}\overrightarrow b ,{\rm{ }}\overrightarrow x ,{\rm{ }}\overrightarrow y ,...$ Vectơ – … [Đọc thêm...] vềBài 1. Các định nghĩa Vecto – Chương 1 – Hình học 10
Ôn tập Chương 3 – Đại số 10
I. Phương trình, hệ phương trình bậc nhất hai ẩn 1. Phương trình bậc nhất Dạng tổng quát: $y=ax+b, (a\neq 0)$ 2. Phương trình bậc nhất hai ẩn Dạng tổng quát: $ax+by=c$ (1) Trong đó: a , b , c là các hệ số. a và b không đồng thời bằng 0. Chú ý: Khi $a=b=0$ = > (1) <=> $0x + 0y = c$. Nếu $c \neq 0$ … [Đọc thêm...] vềÔn tập Chương 3 – Đại số 10
Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn – Chương 3 – Đại số 10
1. Hệ hai phương trình bậc nhất hai ẩn Cho hệ phương trình bậc nhất hai ẩn: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\,\,\,\left( I \right)\,\,\,\left( {{a^2} + {b^2} \ne 0;a{'^2} + b{'^2} \ne 0} \right)\) - Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) đồng thời là nghiệm của cả hai phương trình trong hệ được gọi là một nghiệm của hệ. - … [Đọc thêm...] vềBài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn – Chương 3 – Đại số 10
Bài 2. Phương trình quy về phương trình bậc nhất, bậc hai – Chương 3 – Đại số 10
1. Phương trình bậc nhất \(ax + b = 0\) +) \(a \ne 0\) thì phương trình có nghiệm duy nhất \(x = - \dfrac{b}{a}\) +) \(a = 0\) và $b \ne 0$ thì phương trình vô nghiệm. +) \(a = 0\) và $b = 0$ thì phương trình vô số nghiệm. 2. Phương trình \(a{x^2} + bx + c = 0\) +) \(a = 0\) thì trở thành phương trình \(bx + c = 0\) +) \(a \ne 0\) i) \(\Delta > 0\) thì … [Đọc thêm...] vềBài 2. Phương trình quy về phương trình bậc nhất, bậc hai – Chương 3 – Đại số 10
Bài 1. Đại cương về phương trình – – Chương 3 – Đại số 10
1. Khái niệm phương trình a) Phương trình một ẩn Phương trình ẩn \(x\) là mệnh đề chứa biến có dạng $f\left( x \right) = g\left( x \right)\,\,\left( 1 \right)$ trong đó $f\left( x \right)$ và $g\left( x \right)$ là những biểu thức của $x.$ Ta gọi $f\left( x \right)$ là vế trái, $g\left( x \right)$ là vế phải của phương trình $\left( 1 \right).$ Nếu có số thực … [Đọc thêm...] vềBài 1. Đại cương về phương trình – – Chương 3 – Đại số 10
Ôn tập chương 2 – Đại số 10
I. HÀM SỐ 1. Định nghĩa Cho \(D \subset \mathbb{R},\,\,D \ne \emptyset \). Hàm số \(f\) xác định trên $D$ là một qui tắc đặt tương ứng mỗi số \(x \in D\) với một và chỉ một số \(y \in \mathbb{R}\). 2. Tập xác định Tập xác định của hàm số $y = f\left( x \right)$ là tập hợp tất cả các số thực $x$ sao cho biểu thức \(f\left( x \right)\) có nghĩa. 3. Sự … [Đọc thêm...] vềÔn tập chương 2 – Đại số 10
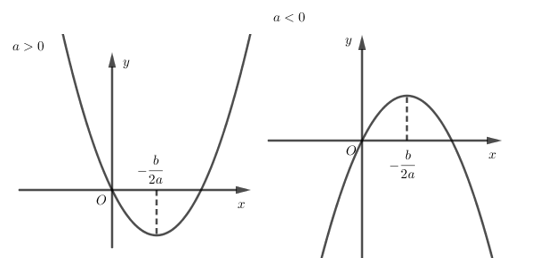
Bài 3. Hàm số bậc hai – Chương 2 – Đại số 10
1. Hàm số bậc hai a. Định nghĩa - Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) - TXĐ: \(D = R\). b. Đồ thị hàm số bậc hai - Có dáng là đường Parabol có đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right),\Delta = {b^2} - 4ac\). - Trục đối xứng là đường thẳng \(x = - … [Đọc thêm...] vềBài 3. Hàm số bậc hai – Chương 2 – Đại số 10