1. Định nghĩa
Tích của vectơ $\overrightarrow a $ với số thực \(k \ne 0\) là một vectơ, kí hiệu là $k\overrightarrow a $, cùng hướng với $\overrightarrow a $ nếu $k > 0$, ngược hướng với $\overrightarrow a $ nếu $k < 0$ và có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\)
Quy ước: $0\overrightarrow a = \overrightarrow 0 $ và $k\overrightarrow 0 = \overrightarrow 0 $
2. Tính chất
$\begin{array}{l}{\rm{ i}}){\rm{ }}(k{\rm{ }} + {\rm{ }}m)\overrightarrow a = k\overrightarrow a + m\overrightarrow a \\ {\rm{ii}}){\rm{ }}k(\overrightarrow a \pm \overrightarrow b ) = k\overrightarrow a \pm k\overrightarrow b \\{\rm{iii}})\,\,k(m\overrightarrow a ){\rm{ }} = {\rm{ }}(km)\overrightarrow a \\{\rm{ iv}})\,\,\,k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}k = 0\\\overrightarrow a = \overrightarrow 0 \end{array} \right.\\{\rm{v) 1}}\overrightarrow a = \overrightarrow a ,\,\,\,( – {\rm{1)}}\overrightarrow a = – \overrightarrow a \end{array}$
3. Điều kiện để hai vectơ cùng phương
+) $\overrightarrow b $ cùng phương $\overrightarrow a $($\overrightarrow a \ne \overrightarrow 0 $) khi và chỉ khi có số \(k\) thỏa $\overrightarrow b = k\overrightarrow a $
+) Điều kiện cần và đủ để $A,B,C$ thẳng hàng là có số $k$ sao cho $\overrightarrow {AB} = k\overrightarrow {AC} $
4. Phân tích một vectơ theo hai vectơ không cùng phương
Cho $\overrightarrow a $ không cùng phương $\overrightarrow b $. Với mọi vectơ $\overrightarrow x $ luôn được biểu diễn $\overrightarrow x = m\overrightarrow a + n\overrightarrow b $ với \(m,\,\,n\) là các số thực duy nhất.
Phương pháp phân tích một véc tơ qua hai véc tơ không cùng phương
Sử dụng các quy tắc ba điểm (xen thêm điểm vào giữa để làm xuất hiện các véc tơ không cùng phương đề bài yêu cầu), các tính chất trung điểm, trọng tâm, tích của một véc tơ với một số để biến đổi làm sao cho xuất hiện.
Một kết quả hay được sử dụng khi phân tích một véc tơ qua hai véc tơ không cùng phương như sau:
Cho đoạn thẳng \(AB\), một điểm \(I \in AB\) thỏa mãn \(\overrightarrow {IA} = k\overrightarrow {IB} \) thì với điểm \(M\) bất kì ta luôn có:
\(\overrightarrow {MI} = \dfrac{{ – 1}}{{k – 1}}\overrightarrow {MA} + \dfrac{k}{{k – 1}}\overrightarrow {MB} \)
Chứng minh:
Ta có:
\(\overrightarrow {MI} = \overrightarrow {MA} + \overrightarrow {AI} \) \( = \overrightarrow {MA} – \overrightarrow {IA} \) \( = \overrightarrow {MA} – k\overrightarrow {IB} \) \( = \overrightarrow {MA} – k\left( {\overrightarrow {IM} + \overrightarrow {MB} } \right)\) \( = \overrightarrow {MA} – k\overrightarrow {IM} – k\overrightarrow {MB} \) \( = \overrightarrow {MA} + k\overrightarrow {MI} – k\overrightarrow {MB} \)
Suy ra \( \overrightarrow {MI}= \overrightarrow {MA} + k\overrightarrow {MI} – k\overrightarrow {MB} \)
\( \Rightarrow \overrightarrow {MI} – k\overrightarrow {MI} = \overrightarrow {MA} – k\overrightarrow {MB} \) \( \Leftrightarrow \left( {1 – k} \right)\overrightarrow {MI} = \overrightarrow {MA} – k\overrightarrow {MB} \) \( \Leftrightarrow \left( {k – 1} \right)\overrightarrow {MI} = – \overrightarrow {MA} + k\overrightarrow {MB} \) \( \Leftrightarrow \overrightarrow {MI} = \dfrac{{ – 1}}{{k – 1}}\overrightarrow {MA} + \dfrac{k}{{k – 1}}\overrightarrow {MB} \) (đpcm)
1. Bài tập cơ bản
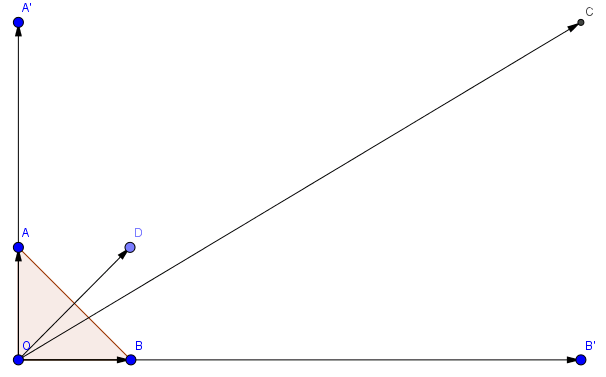
Bài 1: Cho tam giác OAB vuông cân với \(OA=OB=a\). Tính độ dài của các vectơ \(\vec{OA}+\vec{OB}\); \(3\vec{OA}+4\vec{OB}\)
Hướng dẫn:

Do tam giác OAB vuông cân tại O có cạnh là a. Dễ dàng tính được \(\vec{OA}+\vec{OB}\) theo quy tắc hình bình hành, \(\vec{OA}+\vec{OB}=\vec{OD}\)
Độ lớn của \(|\vec{OD}|\)=\(a\sqrt{2}\)
Tương tự, ta tính \(3\vec{OA}+4\vec{OB}\)
Nhận thấy rằng \(3|\vec{OA}|=3a;4|\vec{OB}|=4a\)
Theo quy tắc hình bình hành và theo hình vẽ, ta có \(3\vec{OA}+4\vec{OB}=\vec{OC}\)
Độ lớn của \(|\vec{OC}|=5a\) theo định lý Pytago.
Bài 2: Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có hệ thức: \(\vec{AB}-\vec{AD}=\vec{CB}-\vec{CD}\)
Hướng dẫn:
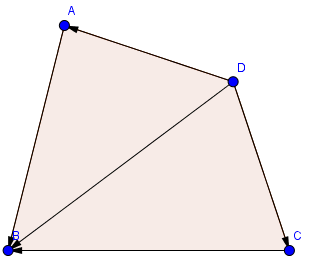
Đề yêu cầu cần chứng minh \(\vec{AB}-\vec{AD}=\vec{CB}-\vec{CD}\)
Ta viết lại: \(\Leftrightarrow \vec{AB}+\vec{DA}=\vec{CB}+\vec{DC}=\vec{DB}\Rightarrow dpcm\)
2. Bài tập nâng cao
Bài 1: Cho hình chữ nhật có \(AB=5cm\), \(BC=10cm\). Tính \(|\vec{AB}+\vec{AC}+\vec{AD}|\)
Hướng dẫn:
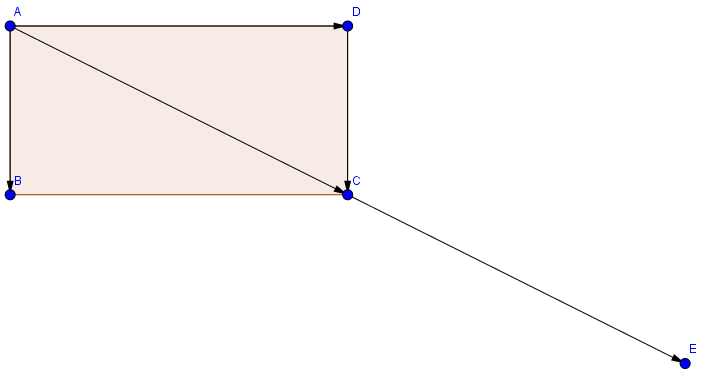
Như hình trên, chúng ta có thể viết lại như sau:
\(\vec{AB}+\vec{AC}+\vec{AD}=\vec{DC}+\vec{AC}+\vec{AD}=\vec{AC}+\vec{AC}=2\vec{AC}\)
Vậy \(|\vec{AB}+\vec{AC}+\vec{AD}|=2|\vec{AC}|\)
Bằng Pytago, ta dễ dàng tính toán được \(2|\vec{AC}|=10\sqrt{5}(cm)\)
Bài 2: Cho tam giác ABC. M là điểm thuộc đoạn BC sao cho \(MB=2MC\). Chứng minh rằng: \(\vec{AM}=\frac{1}{3}\vec{AB}+\frac{2}{3}\vec{AC}\)
Hướng dẫn:
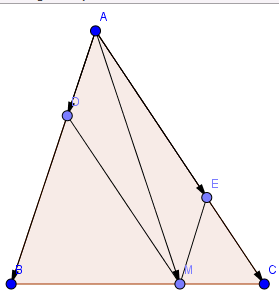
Theo giả thiết, \(MB=2MC\).
Trên AB lấy điểm D sao cho \(AD=\frac{1}{3}AB\), trên AC lấy điểm E sao cho \(CE=\frac{1}{3}AC\)
Vậy, theo đề được viết lại như sau: \(\frac{1}{3}\vec{AB}=\vec{AD};\frac{2}{3}\vec{AC}=\vec{AE}\)
Cần chứng minh ADME là hình bình hành.
Thật vậy, với tỷ lệ đề cho, ta tìm được các cặp cạnh đối song song nhờ định lí Thales đảo.
Vậy: \(\left\{\begin{matrix} AD//ME\\ AE//DM \end{matrix}\right.\) hay ADME là hình bình hành
nên \(\vec{AM}=\frac{1}{3}\vec{AB}+\frac{2}{3}\vec{AC}\)
