1. Tổng hai vectơ
a) Định nghĩa
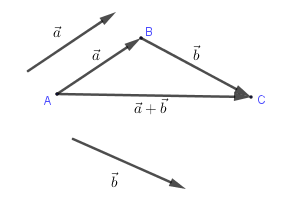
Cho hai vectơ $\overrightarrow a \,;\,\,\overrightarrow b $. Từ điểm A tùy ý vẽ $\overrightarrow {AB} = \overrightarrow a $ rồi từ B vẽ $\overrightarrow {BC} = \overrightarrow b $.
Khi đó vectơ $\overrightarrow {AC} $ được gọi là tổng của hai vectơ $\overrightarrow a \,;\,\,\overrightarrow b $.
Kí hiệu $\overrightarrow {AC} = \overrightarrow a + \overrightarrow b $

b) Tính chất
+ Giao hoán : $\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a $
+ Kết hợp : $\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)$
+ Tính chất vectơ – không: $\overrightarrow a + \overrightarrow 0 = \overrightarrow a {\rm{, }}\forall \overrightarrow a $
2. Các quy tắc
Quy tắc ba điểm: Cho $A,B,C$ tùy ý, ta có : $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $
Quy tắc hình bình hành: Nếu \(ABCD\) là hình bình hành thì $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} $
Ta có thể mở rộng quy tắc ba điểm cho n điểm ${A_1},\,{A_2},\,…,\,{A_n}$ thì $\overrightarrow {{A_1}{A_2}} + \overrightarrow {{A_2}{A_3}} + … + \overrightarrow {{A_{n – 1}}{A_n}} = \overrightarrow {{A_1}{A_n}} $
3. Các điểm đặc biệt
a) Trung điểm
Cho \(I\) là trung điểm \(AB\) và một điểm \(M\) bất kì, khi đó:
+) \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).
+) \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
Ngược lại, nếu có 2 tính chất trên ta cũng suy ra $I$ là trung điểm của $AB$
b) Trọng tâm
Cho \(G\) là trọng tâm tam giác \(ABC\) và \(M\) là một điểm bất kì, khi đó:
+) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
+) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
Chứng minh:
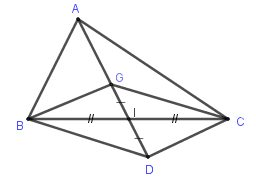
Gọi \(I\) là trung điểm của \(BC\) và \(D\) đối xứng \(G\) qua \(I\)
Khi đó \(BGCD\) là hình bình hành.
Suy ra \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \) (quy tắc hình bình hành)
Mà \(GA = GD = 2GI\) nên \(G\) là trung điểm của \(AD\)
Do đó \(\overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow 0 \) (tính chất trung điểm)
Vậy \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow 0 \)
Với \(M\) là điểm bất kì thì:
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \) \( = \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} \) \( = 3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \)
Ngược lại, nếu có hai tính chất trên ta cũng suy ra ngược lại rằng $G$ là trọng tâm của tam giác.
2. Vectơ đối của một vec tơ
Vectơ đối của vectơ $\overrightarrow a $ là vectơ ngược hướng và có cùng độ dài với vectơ $\overrightarrow a $
Kí hiệu $ – \overrightarrow a $
Như vậy $\overrightarrow a + \left( { – \overrightarrow a } \right) = \overrightarrow 0 {\rm{, }}\forall \overrightarrow a $ và \(\overrightarrow {AB} = – \overrightarrow {BA} \)
3. Định nghĩa hiệu hai vec tơ
Hiệu của hai vectơ $\overrightarrow a $ và $\overrightarrow b $ là tổng của vectơ $\overrightarrow a $ và vectơ đối của vectơ $\overrightarrow b $.
Kí hiệu là $\overrightarrow a – \overrightarrow b = \overrightarrow a + \left( { – \overrightarrow b } \right)$
Quy tắc về hiệu vectơ: Cho $O,A,B$ tùy ý ta có: $\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {AB} $
Bài tập minh họa
1. Bài tập cơ bản
Bài 1: Chứng minh rằng trong một tứ giác nếu \(\vec{AB}=\vec{CD}\) thì \(\vec{AC}=\vec{BD}\)
Hướng dẫn:
Xét trường hợp A, B, C, D thẳng hàng, ta có
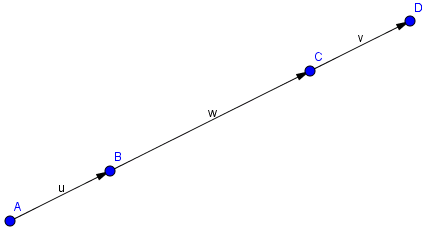
Nhận thấy rằng, khi \(\vec{AB}=\vec{CD}\), theo phép cộng vectơ, ta cộng cho đại lượng vectơ \(\vec{BC}\) ta sẽ ra đpcm.
Xét tứ hình bình hành ABDC bằng hình vẽ sau, ta có:
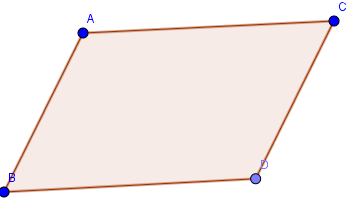
Ta nhận thấy rằng, theo giả thiết \(\vec{AB}=\vec{CD}\) thì AB song song với CD và AB=CD. Ta dễ dàng suy ra được \(\vec{AC}=\vec{BD}\) (dpcm)
Bài 2: Xác định tính đúng sai của mệnh đề: \(|\vec{a}+\vec{b}|=\vec{a}+\vec{b}\)
Hướng dẫn: Nhận thấy rằng điều này chỉ xảy ra khi và chỉ khi 2 vectơ trên cùng hứng ta mới được cộng đại số như vậy
Còn với trường hợp ngược hướng thì hai vectơ sẽ bị triệt tiêu nhau thành dấu “-”
Đối với hai vectơ không cùng phương, ta có hình vẽ sau:
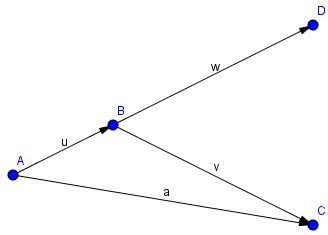
Như hình trên, ta thấy điều khẳng định trên là sai!
Bài 3: Cho hình bình hành ABCD. Chứng minh rằng: \(\vec{DA}-\vec{DB}+\vec{DC}=\vec{0}\)
Hướng dẫn:
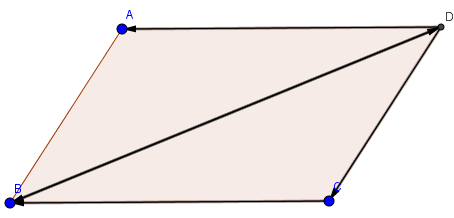
Như hình vẽ, ta thấy :\(\vec{DA}-\vec{DB}+\vec{DC}=\vec{CB}+\vec{BD}+\vec{DC}=\vec{CC}=\vec{0}\)
2. Bài tập nâng cao
Bài 1: Cho hai lực \(\vec{F_1}\) và \(\vec{F_2}\) cùng chung một điểm đặt như hình vẽ. Biết rằng \(\vec{F_1}=\vec{F_2}=200N\). Hãy tìm cường độ lực tổng hợp của chúng.
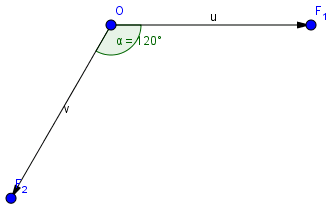
Hướng dẫn:
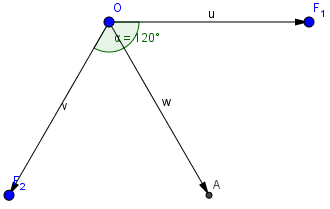
Cường độ tổng hợp lực đó chính là \(\vec{OA}\), và có độ lớn cũng là 100N
Bài 2: Chứng minh rằng \(\vec{AB}=\vec{CD}\) khi và chỉ khi trung điểm của AD và BC trùng nhau.
Hướng dẫn:
Ta xét 2 trường hợp.
Trường hợp 4 điểm A, B, C, D thẳng hàng
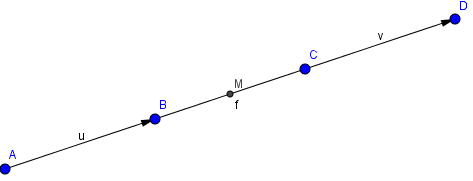
Với trường hợp này, ta dễ dàng thấy được AD và BC có cùng trung điểm M.
Chứng minh bài toán dễ dàng bằng phương pháp cộng đại số.
Trường hợp AB song song CD
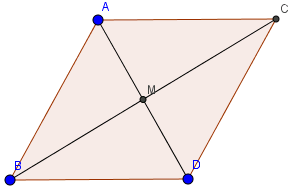
Trường hợp này hai đường chéo AD và BC cắt nhau tại trung điểm mỗi đường. Ta có dpcm.
