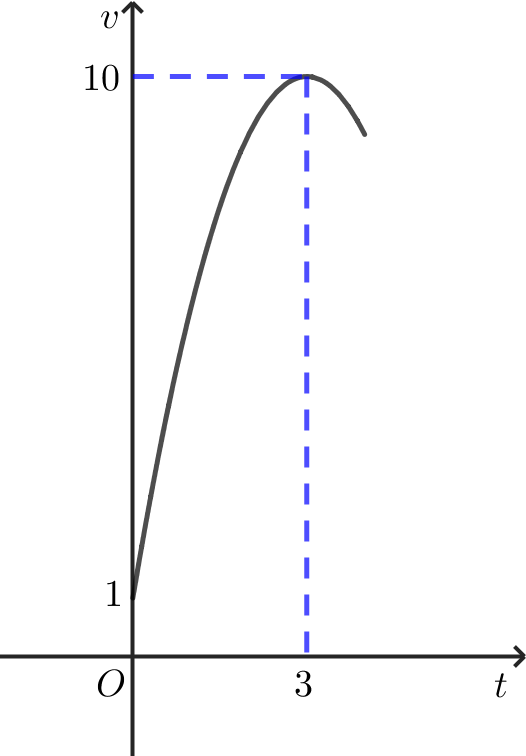
Một vật chuyển động trong 4 giờ với vận tốc $v\left( \text{km/h} \right)$ phụ thuộc vào thời gian $t\left( \text{h} \right)$ có đồ thị vận tốc là một đường parabol có đỉnh $I(3;10)$ và trục đối xứng vuông góc với trục hoành như hình vẽ. Tính quãng đường vật di chuyển được trong nửa thời gian sau của chuyển động đó (kết quả làm tròn đến hàng phần chục và tính theo đơn vị $\text{km}$ )
Lời giải
Đáp số: $19,3$
Dựa vào đồ thị ta tìm được vận tốc $v\left( t \right)=-{{t}^{2}}+6t+1,t\in \left[ 0;4 \right]$.
Quãng đường $s\left( t \right)$ vật di chuyển được trong thời gian 4h là một nguyên hàm của $v\left( t \right),t\in \left[ 0;4 \right]$
Ta có $s\left( t \right)=\int{\left( -{{t}^{2}}+6t+1 \right)\text{d}t}=-\dfrac{{{t}^{3}}}{3}+3{{t}^{2}}+t+C$.
Quãng đường vật di chuyển được trong 2h đầu là $s\left( 2 \right)=\dfrac{34}{3}+C\left( \text{km} \right)$.
Quãng đường vật di chuyển được trong 4h là $s\left( 4 \right)=\dfrac{92}{3}+C\left( \text{km} \right)$.
Quãng đường vật di chuyển được trong nửa thời gian sau của chuyển động là: $s\left( 4 \right)-s\left( 2 \right)=\dfrac{58}{3}\left( \text{km} \right)\approx 19,3\left( \text{km} \right)$.
