Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu chuyển động với vận tốc được biểu thị bằng đồ thị là đường cong parabol như hình bên dưới. Biết rằng sau $5$ phút thì xe đạt đến vận tốc cao nhất $1000$ m/phút và bắt đầu giảm vận tốc, đi được $6$ phút thì xe chuyển động đều.
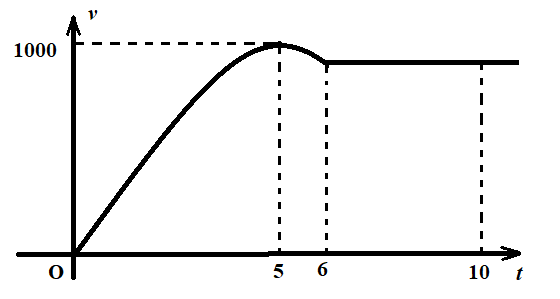
Hỏi quãng đường xe đã đi được trong khoảng 10 phút đầu tiên là bao nhiêu mét?
Lời giải
Trả lời: 8160
Dựa vào đồ thị ta có phương trình vận tốc của ô tô là $v(t)=-40{{t}^{2}}+400t$ với $t\in \left[ 0;6 \right]$ và $v=960$ với $t{>}6$. Trong khoảng 6 phút đầu phương trình quãng đường là $S(t)=\int{\left( -40{{t}^{2}}+400t \right)}dt=-\dfrac{40}{3}{{t}^{3}}+200{{t}^{2}}+C$.
Tại thời điểm xe ô tô xuất phát ta có ${{t}_{0}}=0$ và $S\left( {{t}_{0}} \right)=0$ suy ra $C=0$ nên phương trình quãng đường là $S(t)=-\dfrac{40}{3}{{t}^{3}}+200{{t}^{2}}$.
Trong khoảng 6 phút đầu ô tô đi được quãng đường là $S(6)=4320m$ và 4 phút tiếp theo ô tô đi được quãng đường là $960\text{x4}=3840m$
Vậy quãng đường ô tô đi được trong 10 phút đầu là $4320+3840=8160$ m.
