Một máy bay đang chuyển động thẳng đều trên mặt đất với vận tốc ${v=3({m} / {s})}$ thì bắt đầu tăng tốc với độ biến thiên vận tốc là hàm số ${a(t)}$ có đồ thị hàm số là đường thẳng như hình vẽ.
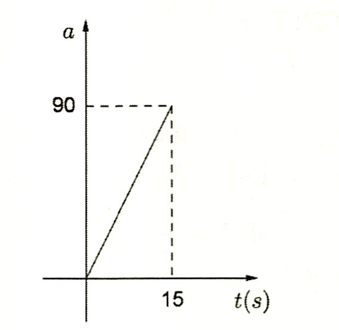
Sau 15s tăng tốc thì máy bay đạt đến vận tốc đủ lớn để phóng khỏi mặt đất. Hãy tính vận tốc (m/s) khi máy bay bắt đầu rời khỏi mặt đất.
Lời giải
Trả lời: 678
Đường thẳng ${a(t)=m t+n}$ đi qua gốc tọa độ ${O(0 ; 0)}$ và điểm ${A(16 ; 90)}$ nên suy ra
${\left\{\begin{array} { l }
{ m . 0 + n = 0 } \\
{ m . 1 5 + n = 9 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
n=0 \\
m=6
\end{array} \Rightarrow a(t)=6 t .\right.\right.
}$
Ta hiểu rằng, nguyên hàm của gia tốc ${a(t)}$ chính là vận tốc của vật chuyển động. Do đó ta có ${v(t)=\int a(t) d t=\int 6 t d t=3 t^2+C .
}$
Tại thời điểm bắt đầu tăng tốc thì xem như ${t=0}$ và vận tốc lúc đó là ${v=3({m} / {s})
}$
Suy ra ${v(0)=3 \Leftrightarrow 3.0^2+C=3 \Leftrightarrow C=3 \Rightarrow v(t)=3 t^2+3}$.
Vậy vận tốc máy bay đạt được khi bắt đầu phóng khỏi mặt đất là
${v(15)=3 \cdot 15^2+3=678({m} / {s}) \text {. }
}$
