Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây và ${s}$ là quãng đường chuyển động được của vật trong ${t}$ giây tính bằng mét

Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây và ${s}$ là quãng đường chuyển động được của vật trong ${t}$ giây tính bằng mét. Khi đó:

a) Vận tốc của vật tại thời điểm ${t=2}$ là ${v(2)=s^{\prime}(2)=8({m} / {s})}$.

b) Gia tốc của vật tại thời điểm ${t=2}$ là ${a(2)=v^{\prime}(2)=s^{\prime \prime}(2)=6 \cdot 2-6=6\left({m} / {s}^2\right)}$.

c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng ${16 {m} / {s}^2}$ là $12\left({m} / {s}^2\right)$.

d) Thời điểm ${t=1}$ (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.

Lời giải: Ta có: $s^{\prime}\left( t \right)=3{{t}^{2}}-6t+7$ và $s^{\prime\prime}\left( t \right)=6t-6$.
Vận tốc của vật tại thời điểm ${t=2}$ là: $v\left( 2 \right)=s^{\prime}\left( 2 \right)=3 \cdot 2^{2}-6 \cdot 2+7=7({m}/{s})$.
Gia tốc của vật tại thời điểm ${t=2}$ là: $a\left( 2 \right)=v^{\prime}\left( 2 \right)=s^{\prime\prime}\left( 2 \right)=6 \cdot 2-6=6\left({m}/{s}^2\right)$.
Vận tốc của chuyển động bằng ${16 {m} / {s}^2}$ tại thời điểm ${t}$ nghĩa là:
$v\left( t \right)=s^{\prime}\left( t \right)=16\Leftrightarrow 3{{t}^{2}}-6t+7=16\Leftrightarrow \left[ \begin{array}{*{35}{l}} t=3\text{ (tho }\hat{\mathrm{u}}\text{ a ma }\tilde{\mathrm{o}}\text{ n) } \\ t=-1\text{ (loa }\ddot{\mathrm{i}}\text{ i) } \end{array} \right]$.
Gia tốc của vật tại thời điểm ${t=3}$ là: $a\left( 3 \right)=v^{\prime}\left( 3 \right)=s^{\prime\prime}\left( 3 \right)=6 \cdot 3-6=12\left({m}/{s}^2\right)$.
Vận tốc của chuyển động có phương trình $v\left( t \right)=3{{t}^{2}}-6t+7$.
Có $v^{\prime}\left( t \right)=6t-6=0\Leftrightarrow t=1$.
Bảng biến thiên

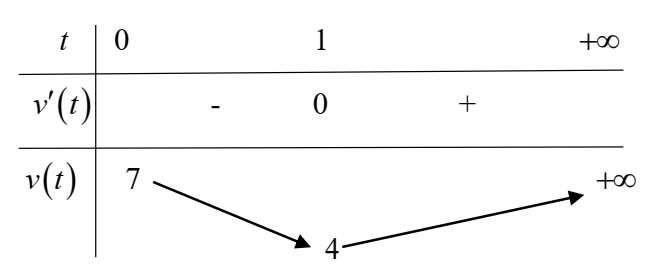
Từ bảng biến thiên suy ra hàm số có giá trị nhỏ nhất bằng 4 tại ${t=1}$.
Vậy tại thời điểm ${t=1}$ thì vận tốc của chuyển động đạt giá trị nhỏ nhất bằng $4({m}/{s})$.
(Sai) Vận tốc của vật tại thời điểm ${t=2}$ là ${v(2)=s^{\prime}(2)=8({m} / {s})}$.
(Vì): Vận tốc của vật tại thời điểm ${t=2}$ là ${v(2)=s^{\prime}(2)=3 \cdot 2^2-6 \cdot 2+7=7({m} / {s})}$.
(Đúng) Gia tốc của vật tại thời điểm ${t=2}$ là ${a(2)=v^{\prime}(2)=s^{\prime \prime}(2)=6 \cdot 2-6=6\left({m} / {s}^2\right)}$.
(Đúng) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng ${16 {m} / {s}^2}$ là $12\left({m} / {s}^2\right)$.
(Vì): Vận tốc của chuyển động bằng ${16 {m} / {s}^2}$ tại thời điểm ${t}$ nghĩa là:
$v\left( t \right)=s^{\prime}\left( t \right)=16\Leftrightarrow 3{{t}^{2}}-6t+7=16\Leftrightarrow \left[ \begin{array}{*{35}{l}} t=3\text{ (tho }\hat{\mathrm{u}}\text{ a ma }\tilde{\mathrm{o}}\text{ n) } \\ t=-1\text{ (loa }\ddot{\mathrm{i}}\text{ i) } \end{array} \right.$.
Gia tốc của vật tại thời điểm ${t=3}$ là: $a\left( 3 \right)=v^{\prime}\left( 3 \right)=s^{\prime\prime}\left( 3 \right)=6 \cdot 3-6=12\left({m} / {s}^2\right)$.
(Đúng) Thời điểm ${t=1}$ (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.