Khi nuôi tôm thẻ trong ao, một kỹ sư thủy sản đã thống kê được nếu mỗi mét vuông mặt ao thả $x$ con tôm giống thì cuối mỗi vụ con tôm có cân nặng trung bình là $108-{{x}^{2}}$.
a) Để lượng tôm thu được tăng lên thì mật độ tôm giống thả vào ao là từ 6 đến 10 con/ ${{m}^{2}}$.
b) Sau mỗi vụ khối lượng tôm trung bình trong mỗi mét vuông mặt ao là $\left( 108-{{x}^{2}} \right)x$.
c) Khi thả 10 con tôm giống / ${{m}^{2}}$ thì lượng tôm thu được là $0,08kg/{{m}^{2}}$.
d) Để sản lượng tôm lớn nhất thì nên thả 7 con tôm/ ${{m}^{2}}$.
Lời giải: Khối lượng tôm trung bình trong mỗi mét vuông ao nuôi là $M\left( x \right)=\left( 108-{{x}^{2}} \right)x$.
Để tôm phát triển được, $x{>}0;{{x}^{2}}\le 108$ nên $0{
Xét hàm số $M\left( x \right)=\left( 108-{{x}^{2}} \right)x=-{{x}^{3}}+108x$.
Có ${M}’\left( x \right)=-3{{x}^{2}}+108=-3\left( {{x}^{2}}-36 \right)$; ${M}’\left( x \right)=0\Rightarrow x=6$.
Ta có bảng biến thiên:
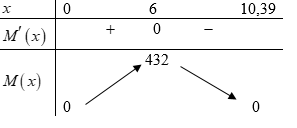
Để sản lượng tôm lớn nhất thì nên thả 6 con tôm/ ${{m}^{2}}$.
Lượng tôm thu được tăng lên khi hàm số $M\left( x \right)$ đồng biến. Dựa vào bảng biến thiên ta có $x\in \left( 0;6 \right)$, hay mật độ tôm không quá 6 con/ ${{m}^{2}}$.
(Sai) Để lượng tôm thu được tăng lên thì mật độ tôm giống thả vào ao là từ 6 đến 10 con/ ${{m}^{2}}$.
(Vì): Lượng tôm thu được tăng lên khi hàm số $M\left( x \right)$ đồng biến. Dựa vào bảng biến thiên ta có $x\in \left( 0;6 \right)$, hay mật độ tôm không quá 6 con/ ${{m}^{2}}$.
(Đúng) Sau mỗi vụ khối lượng tôm trung bình trong mỗi mét vuông mặt ao là $\left( 108-{{x}^{2}} \right)x$.
(Vì): Khối lượng tôm trung bình trong mỗi mét vuông ao nuôi là $M\left( x \right)=\left( \text{cân nặng trung bình} \right) \cdot \left( \text{số con tôm} \right) = \left( 108-{{x}^{2}} \right)x$. Đây là công thức đúng dựa trên đề bài đã cho.
(Đúng) Khi thả 10 con tôm giống / ${{m}^{2}}$ thì lượng tôm thu được là $0,08kg/{{m}^{2}}$.
(Vì): Khi $x=10$, khối lượng tôm thu được là $M\left( 10 \right)=\left( 108-{{10}^{2}} \right) \cdot 10 = \left( 108-100 \right) \cdot 10 = 8 \cdot 10 = 80 \text{ gam} = 0,08 \text{ kg}$.
(Sai) Để sản lượng tôm lớn nhất thì nên thả 7 con tôm/ ${{m}^{2}}$.
(Vì): Xét hàm số $M\left( x \right)=-{{x}^{3}}+108x$ với $0{}0$). Bảng biến thiên cho thấy $M(x)$ đạt giá trị lớn nhất tại $x=6$. Vì vậy, thả 7 con tôm/ ${{m}^{2}}$ sẽ không cho sản lượng lớn nhất.
