Một cơ sở đóng giầy sản xuất mỗi ngày được $x$ đôi giầy

Một cơ sở đóng giầy sản xuất mỗi ngày được $x$ đôi giầy. $1\le x\le 20$. Tổng chi phí sản xuất $x$ đôi giầy là $C\left( x \right)={{x}^{3}}-6{{x}^{2}}-88x+592$. Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá $200$ nghìn đồng /một đôi. Gọi $T\left( x \right)$ là số tiền bán được và $L\left( x \right)$ là lợi nhuận thu được sau khi bán hết $x$ đôi giầy.
Các mệnh đề sau đúng hay sai?

a) Lợi nhuận tối đa thu được trong một ngày là $2000$ nghìn đồng.
.

b) Cơ sở này sản xuất được $10$ đôi giầy thì lợi nhuận thu được là nhiều nhất.
.

c) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là $1584$ khi đó cơ sở phải sản xuất được $9$ đôi giầy.
.

d) Giả sử trong một ngày nào đó cơ sở sản xuất được $10$ đôi giầy thì lợi nhuận thu được là $1900$.
.

Lời giải: Lợi nhuận thu được là $L\left( x \right)=T\left( x \right)-C\left( x \right)=-{{x}^{3}}+6{{x}^{2}}+288x-592$.
Một ngày nào đó cơ sở sản xuất được $10$ đôi giầy thì lợi nhuận thu được là: $L\left( 10 \right)=-{{10}^{3}}+{{6.10}^{2}}+288.10-592=1888$. Chọn đúng.Lợi nhuận thu được là $1584$, khi đó ta có $1584=-{{x}^{3}}+6{{x}^{2}}+288x-592$
$\Leftrightarrow {{x}^{3}}-6{{x}^{2}}-288x+2176=0\Leftrightarrow \left[ \begin{array}{l} x=-1+\sqrt{273} \\ x=-1-\sqrt{273} \\ x=8 \end{array} \right.$.
Chọn sai.Xét hàm số $L\left( x \right)=-{{x}^{3}}+6{{x}^{2}}+288x-592$ với $1\le x\le 20$.
${L}’\left( x \right)=-3{{x}^{2}}+12x+288$
${L}’\left( x \right)=0\Leftrightarrow -3{{x}^{2}}+12x+288=0\Leftrightarrow \left[ \begin{array}{l} x=12 \\ x=-8(l) \end{array} \right.$
Bảng biến thiên

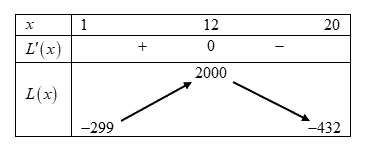
Vậy cơ sở sản xuất được $12$ đôi giầy thì lợi nhuận đạt cao nhất. Chọn đúng.Khi đó lợi nhuận tối đa đạt được trong một ngày là $1980$. Chọn sai.
(Đúng) Lợi nhuận tối đa thu được trong một ngày là $2000$ nghìn đồng.

(Vì): Lợi nhuận $L\left( x \right)=T\left( x \right)-C\left( x \right)=200x-\left( {{x}^{3}}-6{{x}^{2}}-88x+592 \right)=-{{x}^{3}}+6{{x}^{2}}+288x-592$. Ta có ${L}’\left( x \right)=-3{{x}^{2}}+12x+288$. Giải ${L}’\left( x \right)=0$ với $1\le x\le 20$ ta được $x=12$. Lợi nhuận tối đa đạt được tại $x=12$ là $L(12) = -{{(12)}^{3}}+6{{(12)}^{2}}+288(12)-592 = -1728+864+3456-592 = 2000$ nghìn đồng.
(Sai) Cơ sở này sản xuất được $10$ đôi giầy thì lợi nhuận thu được là nhiều nhất.

(Vì): Lợi nhuận $L\left( x \right)=-{{x}^{3}}+6{{x}^{2}}+288x-592$. Ta có ${L}’\left( x \right)=-3{{x}^{2}}+12x+288$. Giải ${L}’\left( x \right)=0$ với $1\le x\le 20$ ta được $x=12$. Lợi nhuận cao nhất đạt được tại $x=12$. Với $x=10$, lợi nhuận là $L(10) = -{{(10)}^{3}}+6{{(10)}^{2}}+288(10)-592 = 1888$, không phải là lớn nhất.
(Sai) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là $1584$ khi đó cơ sở phải sản xuất được $9$ đôi giầy.

(Vì): Để lợi nhuận thu được là $1584$, ta giải phương trình $L\left( x \right)=1584 \Leftrightarrow -{{x}^{3}}+6{{x}^{2}}+288x-592=1584 \Leftrightarrow {{x}^{3}}-6{{x}^{2}}-288x+2176=0$. Phương trình này có một nghiệm nguyên là $x=8$ (thỏa mãn $1\le x\le 20$). Vậy cơ sở phải sản xuất $8$ đôi giầy, không phải $9$ đôi.
(Sai) Giả sử trong một ngày nào đó cơ sở sản xuất được $10$ đôi giầy thì lợi nhuận thu được là $1900$.

(Vì): Với $x=10$ đôi giầy, lợi nhuận thu được là $L\left( 10 \right)=-{{(10)}^{3}}+6{{(10)}^{2}}+288(10)-592=-1000+600+2880-592=1888$ nghìn đồng. Do đó, $1900$ là giá trị sai.