Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng pickleball

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng pickleball. Công ty này sở hữu một số máy sản suất bóng, mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ.

a) Trong 1 giờ, cần 266 máy để sản xuất được 8000 quả bóng pickleball.

b) Trong $\dfrac{8}{3}$ giờ, cần 120 máy để sản xuất được 8000 quả bóng pickleball.

c) Chi phí hoạt động thấp nhất là 6,5 triệu đồng.

d) Để chi phí hoạt động thấp nhất, công ty cần sử dụng 15 máy.

Lời giải: Mỗi máy có thể sản xuất 30 quả bóng trong 1 giờ.
Cần $a$ máy để sản xuất 8000 quả bóng trong 1 giờ.
$\Rightarrow a=\dfrac{8000}{30}=\dfrac{800}{3}\approx 266,67$.Đúng.
Mỗi máy có thể sản xuất 30 quả bóng trong 1 giờ.
Trong $\dfrac{8}{3}$ giờ, mỗi máy có thể sản xuất $\dfrac{8}{3}.30=80$ quả bóng.
Cần $b$ máy để sản xuất 8000 quả bóng trong $\dfrac{8}{3}$ giờ.
$\Rightarrow b=\dfrac{8000}{80}=100$.
Vậy trong $\dfrac{8}{3}$ giờ, cần 100 máy để sản xuất được 8000 quả bóng pickleball.Sai.
Gọi số máy công ty sử dụng để sản xuất là $x\left( x\in {{\mathbb{N}}^{*}} \right)$.
Thời gian cần để sản xuất hết $8000$ quả bóng là: $\dfrac{8000}{30x}$.
Tổng chi phí để sản xuất là: $P\left( x \right)=200x+\dfrac{8000}{30x}.192=200x+\dfrac{51200}{x}$.
Ta có:
${P}’\left( x \right)=200-\dfrac{51200}{{{x}^{2}}}=0\Leftrightarrow \dfrac{200{{x}^{2}}-51200}{{{x}^{2}}}=0\Leftrightarrow 200{{x}^{2}}-51200=0\Leftrightarrow \left[ \begin{array}{l} x=16(n) \\ x=-16\left( l \right) \end{array} \right.$.

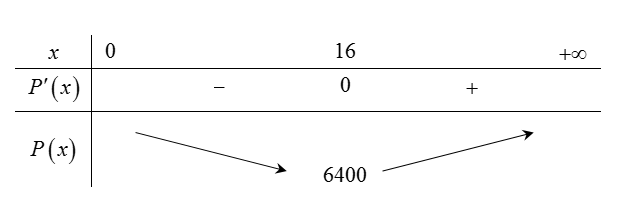
Vậy chi phí hoạt động thấp nhất là 6,4 triệu đồng.Đúng.
Từ bảng biến thiên trên, ta thấy công ty cần sử dụng $16$ máy để chi phí hoạt động là thấp nhất.
(Sai) Trong 1 giờ, cần 266 máy để sản xuất được 8000 quả bóng pickleball.
(Vì): Để sản xuất 8000 quả bóng trong 1 giờ, số máy cần là $\dfrac{8000}{30} = \dfrac{800}{3} \approx 266,67$ máy. Do đó, 266 máy là không đủ.
(Sai) Trong $\dfrac{8}{3}$ giờ, cần 120 máy để sản xuất được 8000 quả bóng pickleball.
(Vì): Mỗi máy có thể sản xuất 30 quả bóng trong 1 giờ. Trong $\dfrac{8}{3}$ giờ, mỗi máy có thể sản xuất $30 \cdot \dfrac{8}{3} = 80$ quả bóng. Để sản xuất 8000 quả bóng, số máy cần là $\dfrac{8000}{80} = 100$ máy, không phải 120 máy.
(Sai) Chi phí hoạt động thấp nhất là 6,5 triệu đồng.
(Vì): Tổng chi phí sản xuất $P(x) = 200x + \dfrac{51200}{x}$. Chi phí thấp nhất đạt được khi $x=16$ máy, $P(16) = 200 \cdot 16 + \dfrac{51200}{16} = 3200 + 3200 = 6400$ nghìn đồng, tức là 6,4 triệu đồng.
(Sai) Để chi phí hoạt động thấp nhất, công ty cần sử dụng 15 máy.
(Vì): Chi phí sản xuất là hàm số $P(x) = 200x + \dfrac{51200}{x}$. Để tìm chi phí thấp nhất, ta tìm đạo hàm $P'(x) = 200 – \dfrac{51200}{x^2}$. Đặt $P'(x) = 0 \Rightarrow 200x^2 = 51200 \Rightarrow x^2 = 256 \Rightarrow x=16$ (do $x{>}0$). Bảng biến thiên cho thấy $x=16$ là điểm cực tiểu của hàm chi phí, không phải 15 máy.