Cho hàm số $y=f(x)=\dfrac{x^2+4x+4}{-x+3}$. Xét tính đúng sai của các phát biểu sau:

Cho hàm số $y=f(x)=\dfrac{x^2+4x+4}{-x+3}$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.
b) $y^{\prime}=\dfrac{-x^2+6x-16}{(-x+3)^2}$.
c) Hàm số $y=f(x)$ đồng biến trên $(-2;3)$.
d) Hàm số $y=f(x)$ nghịch biến trên $(3;8)$.

Lời giải:

$y^{\prime}=\dfrac{-x^2+6x+16}{(-x+3)^2}$. $y^{\prime}=0\Leftrightarrow x_1=-2,x_2=8$.

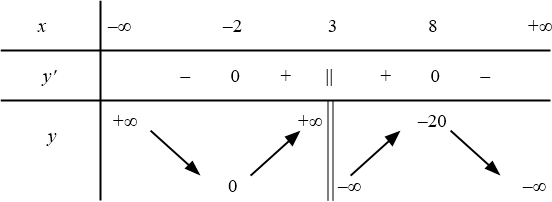
(Đúng) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$. (Vì): $-x+3\neq 0\Leftrightarrow x\neq 3$ nên $D=\mathbb{R}\backslash \left\{3\right\}$.
(Sai) $y^{\prime}=\dfrac{-x^2+6x-16}{(-x+3)^2}$. (Vì): $y^{\prime}=\dfrac{adx^2+2aex+be-cd}{(dx+e)^2}=\dfrac{-x^2+6x+16}{(-x+3)^2}$.
(Đúng) Hàm số $y=f(x)$ đồng biến trên $(-2;3)$.
(Sai) Hàm số $y=f(x)$ nghịch biến trên $(3;8)$.