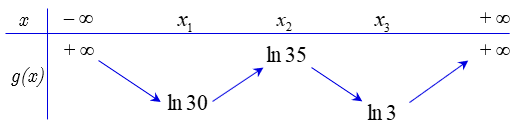
Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau:

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau:

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

A. \(\left( {33;35} \right)\). B. \(\left( {37;40} \right)\). C. \(\left( {29;32} \right)\). D. \(\left( {24;26} \right)\).

Lời giải

Theo bảng biến thiên ta có \(g\left( x \right) = \ln f\left( x \right) \ge \ln 3,\forall x \in \mathbb{R} \Rightarrow f\left( x \right) \ge 3,\forall x \in \mathbb{R}\).

Ta có: \(g’\left( x \right) = {\left[ {\ln f\left( x \right)} \right]^\prime } = \frac{{f’\left( x \right)}}{{f\left( x \right)}} \Rightarrow f’\left( x \right) = g’\left( x \right).f\left( x \right)\)

Nên \(f’\left( x \right) = g’\left( x \right) \Leftrightarrow g’\left( x \right).f\left( x \right) = g’\left( x \right) \Leftrightarrow g’\left( x \right)\left[ {f\left( x \right) – 1} \right] = 0 \Leftrightarrow g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\\x = {x_3}\end{array} \right.\).

Khi đó, diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) là

\(S = \int\limits_{{x_1}}^{{x_2}} {\left| {f’\left( x \right) – g’\left( x \right)} \right|} {\rm{d}}x + \int\limits_{{x_2}}^{{x_3}} {\left| {f’\left( x \right) – g’\left( x \right)} \right|} {\rm{d}}x = \int\limits_{{x_1}}^{{x_2}} {\left| {f’\left( x \right)\left( {1 – \frac{1}{{f\left( x \right)}}} \right)} \right|} {\rm{d}}x + \int\limits_{{x_2}}^{{x_3}} {\left| {f’\left( x \right)\left( {1 – \frac{1}{{f\left( x \right)}}} \right)} \right|} {\rm{d}}x\)

Đặt \(t = f\left( x \right) \Rightarrow dt = f’\left( x \right)dx\).

Đổi cận: \(x = {x_1} \Rightarrow t = 30\), \(x = {x_2} \Rightarrow t = 35\), \(x = {x_3} \Rightarrow t = 3\).

Khi đó, \(S = \left| {\int\limits_{30}^{35} {\left( {1 – \frac{1}{t}} \right)} dt} \right| + \left| {\int\limits_{35}^3 {\left( {1 – \frac{1}{t}} \right)} dt} \right| = \left| {\left. {\left( {t – \ln \left| t \right|} \right)} \right|_{30}^{35}} \right| + \left| {\left. {\left( {\ln \left| t \right| – t} \right)} \right|_3^{35}} \right|\)

\( = \left| {\left( {35 – \ln 35} \right) – \left( {30 – \ln 30} \right)} \right| + \left| {\left( {35 – \ln 35} \right) – \left( {3 – \ln 3} \right)} \right|\)

\( = 5 – \ln 35 + \ln 30 + 32 – \ln 35 + \ln 3 = 37 + \ln \frac{{90}}{{1225}} \approx 34,39\).

=========== Đây là các câu VD-VDC trong đề Toán 2022.