Đề toán 2022 Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

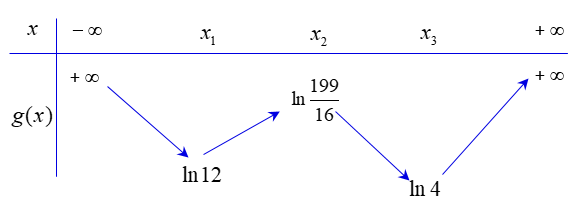
Đề toán 2022 Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

A. \(\left( {7;8} \right)\). B. \(\left( {6;7} \right)\). C. \(\left( {8;9} \right)\). D. \(\left( {10;11} \right)\).

Lời giải

Chọn A

Từ BBT của \(g\left( x \right)\) ta có \(\ln f\left( x \right) \ge \ln 4 \Leftrightarrow f\left( x \right) \ge 4;\forall x \in R\).

Ta có \(g’\left( x \right) = \frac{{f’\left( x \right)}}{{f\left( x \right)}}\).

Xét phương trình \(f’\left( x \right) = g’\left( x \right) \Leftrightarrow \left[ \begin{array}{l}f’\left( x \right) = 0\,\,(*)\\f\left( x \right) = 1\,\,\,(**)\end{array} \right.\)

Do \(f\left( x \right) \ge 4;\forall x \in R\) suy ra phương trình \((**)\) vô nghiệm.

Từ đó suy ra \(f’\left( x \right) = 0 \Leftrightarrow g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\\x = {x_3}\end{array} \right.\).

Mặt khác \(f’\left( x \right) – g’\left( x \right) = f’\left( x \right).\left[ {1 – \frac{1}{{f\left( x \right)}}} \right]\).

Ta có bảng xét dấu

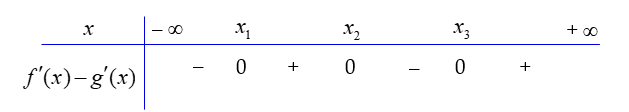
Vậy \(S = \int\limits_{{x_1}}^{{x_3}} {\left| {f’\left( x \right) – g’\left( x \right)} \right|{\rm{d}}x = } \int\limits_{{x_1}}^{{x_2}} {\left[ {f’\left( x \right) – g’\left( x \right)} \right]{\rm{d}}x – \int\limits_{{x_2}}^{{x_3}} {\left[ {f’\left( x \right) – g’\left( x \right)} \right]{\rm{d}}x} } \)

\( = \left[ {f\left( x \right) – g\left( x \right)} \right]\left| {\mathop {}\limits_{{x_1}}^{{x_2}}  – } \right.\left[ {f\left( x \right) – g\left( x \right)} \right]\left| {\mathop {}\limits_{{x_2}}^{{x_3}} } \right.\)

\( = 2f\left( {{x_2}} \right) – f\left( {{x_1}} \right) – f\left( {{x_3}} \right) – 2\ln f\left( {{x_2}} \right) + \ln f\left( {{x_1}} \right) + \ln f\left( {{x_3}} \right)\)

\( = 2\frac{{199}}{{16}} – 12 – 4 – 2\ln \frac{{199}}{{16}} + \ln 12 + \ln 4 \approx 7,704 \in \left( {7;8} \right)\).

=========== Đây là các câu VD-VDC trong đề Toán 2022.