Đề bài: Để trang trí tòa nhà người ta vẽ lên tường một hình như sau: trên mỗi cạnh hình lục giác đều có cạnh là 2dm là một cánh hoa hình parabol mà đỉnh parabol (P) cách các cạnh lục giác là 3dm và nằm phía ngoài lục giác; 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường (P) đó. Hãy tính diện tích hình trên (kể cả lục giác).

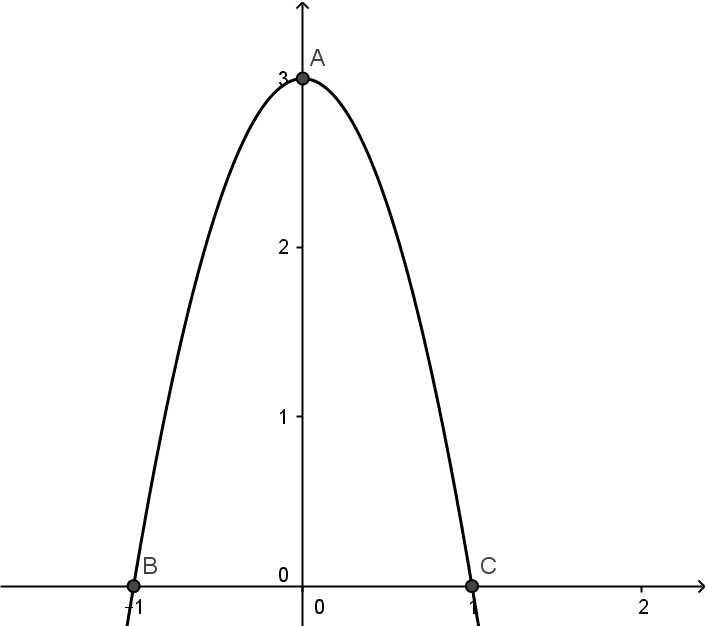
Xét cánh hoa hình parabol (P) đi qua các điểm \(A\left( {0;3} \right),\,\,B\left( { – 1;0} \right),\,\,C\left( {1;0} \right)\) với A là đỉnh của (P) và B, C là hai đầu mút thỏa mãn BC = 2 là độ dài cạnh của hình lục giác đều

Gọi phương trình parabol (P) là \(y = a{x^2} + bx + c\), điểm \(A,\,B,\,C \in \left( P \right) \Rightarrow \left( P \right):y = 3 – 3{x^2}\)

Diện tích cánh hoa được giới hạn bởi \(y = 3 – 3{x^2}\), trục hoành và hai đường thẳng \(x = 1,\,x =  – 1\) là

\({S_0} = \int\limits_{ – 1}^1 {\left| {3 – 3{x^2}} \right|dx}  = 3\int\limits_{ – 1}^1 {\left( {1 – {x^2}} \right)dx}  = 3\left( {x – \frac{{{x^3}}}{3}} \right)\left| {\mathop {}\limits_{ – 1}^1  = 4} \right.\)

“Diện tích lục giác đều cạnh a bằng 6 lần diện tích tam giác đề cạnh a”

Vậy diện tích cần tìm là tổng diện tích cảu sáu cánh hoa ứng với sáu cạnh của lục giác cộng với diện tích của lục giác đều và bằng \(S = 6.4 + 6.\frac{{{2^2}\sqrt 3 }}{4} = 6\sqrt 3  + 24\,d{m^2}.\)