Bài toán gốc Đồ thị hàm số $y=\dfrac{4 x^{2} - 7 x - 4}{x + 6}$ có tâm đối xứng là $I(h;k)$. Giá trị của biểu thức $P=h+2k$ bằngA. $P=-118$.B. $P=-119$.C. $P=-117$.D. $P=-116$.Lời giải: Ta có $a=\underset{x\to +\infty }{\lim }\dfrac{f(x)}{x}=\underset{x\to +\infty }{\lim }\dfrac{4 x^{2} - 7 x - 4}{x \left(x + 6\right)}=4$.$b=\underset{x\to +\infty }{\lim … [Đọc thêm...] vềĐồ thị hàm số $y=\dfrac{4 x^{2} – 7 x – 4}{x + 6}$ có tâm đối xứng là $I(h;k)$. Giá trị của biểu thức $P=h+2k$ bằng
Trắc nghiệm Đồ thị Hàm số
Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 8 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ như hình vẽ dưới đây biết rằng bờ sông là đường thẳng $CD$ không phải rào lưới.
Bài toán gốc Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 8 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ như hình vẽ dưới đây biết rằng bờ sông là đường thẳng $CD$ không phải rào lưới. Hỏi bác nông dân đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?A. $\dfrac{3\sqrt{3}}{4}$.B. $64\sqrt{3}$.C. $48 … [Đọc thêm...] vềMột bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 8 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ như hình vẽ dưới đây biết rằng bờ sông là đường thẳng $CD$ không phải rào lưới.
Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:
Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Số giá trị nguyên $m$ để phương trình $f(x)=m+4$ có 4 nghiệm?A. $9$.B. $4$.C. $3$.D. $6$. Phân tích và Phương pháp giải Dạng bài toán nhận biết số nghiệm của phương trình $f(x)=k$ dựa vào bảng biến thiên (BBT) của hàm số $y=f(x)$. Số nghiệm của phương trình $f(x)=k$ bằng số … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:
Toạ độ giao điểm của đồ thị hàm số $y=\dfrac{x + 2}{- 7 x – 2}$ với trục tung là
Bài toán gốc Toạ độ giao điểm của đồ thị hàm số $y=\dfrac{x + 2}{- 7 x - 2}$ với trục tung làA. $\left(0;0 \right)$.B. $\left(0;-1 \right)$.C. $\left(0;4 \right)$.D. $\left(0;1 \right)$.Lời giải: Cho $x=0$ ta được $y=-1$.Vậy toạ độ giao điểm của đồ thị hàm số với trục tung là $(0;-1)$. Phân tích và Phương pháp giải Dạng bài toán: Tìm tọa độ giao … [Đọc thêm...] vềToạ độ giao điểm của đồ thị hàm số $y=\dfrac{x + 2}{- 7 x – 2}$ với trục tung là
Hàm số nào dưới đây có bảng biến thiên như sau?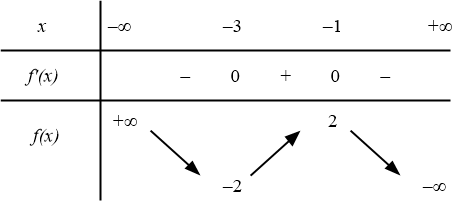

Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y=x^3-6x^2-9x+2$.B. $y=x^3+6x^2+9x+2$.C. $y=-x^3+6x^2+9x-2$.D. $y=-x^3-6x^2-9x-2$. Phân tích và Phương pháp giải Dạng toán: Nhận dạng hàm số bậc ba $y = ax^3 + bx^2 + cx + d$ thông qua bảng biến thiên (BBT). Phương pháp giải: 1. Quan sát giới hạn (khi $x \to \pm\infty$) để xác định … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây: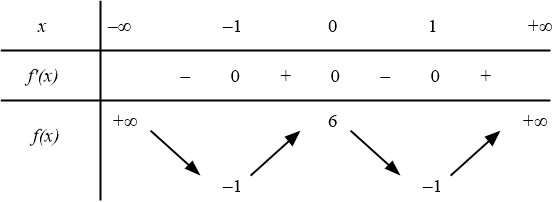

Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x)-5=m$ có 3 nghiệm hoặc 4 nghiệm?A. $6$.B. $7$.C. $10$.D. $9$. Phân tích và Phương pháp giải Dạng toán này yêu cầu biện luận số nghiệm của phương trình chứa tham số dựa trên đồ thị/Bảng biến thiên (BBT) của hàm số $y=f(x)$. … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Đồ thị dưới đây là của hàm số nào?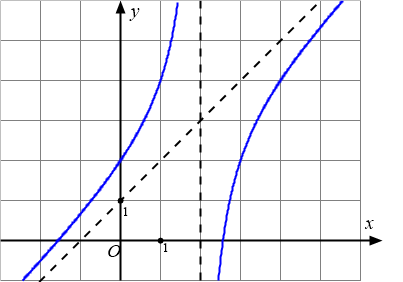

Bài toán gốc Đồ thị dưới đây là của hàm số nào?A. $y=\dfrac{x^2-2x+1}{x}$.B. $y=\dfrac{x^2-x-4}{x-2}$.C. $y=\dfrac{x^2+3x-3}{x+1}$.D. $y=\dfrac{x^2}{-x+1}$.Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.Còn lại hai hàm Phân thức bậc hai chia bậc hai có cùng tiệm cận đứng và tiệm cận … [Đọc thêm...] vềĐồ thị dưới đây là của hàm số nào?

Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có bảng biến thiên như sau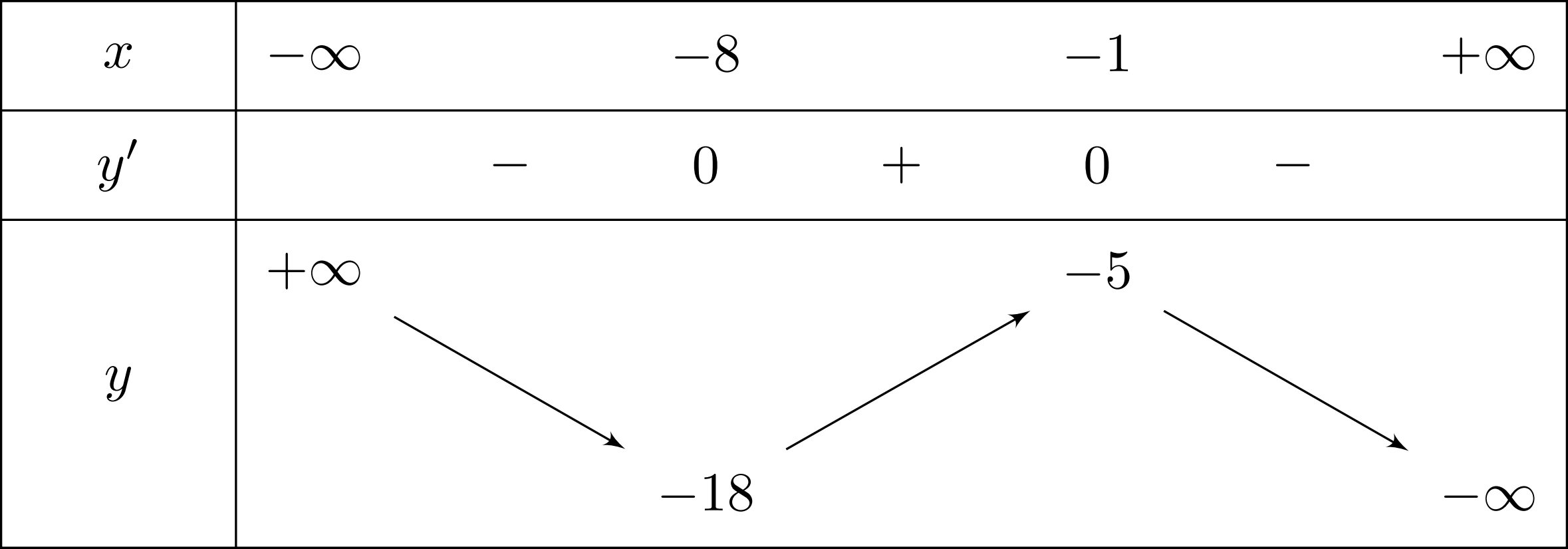
Khẳng định nào dưới đây đúng?

Khẳng định nào dưới đây đúng?
Bài toán gốc Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có bảng biến thiên như sauKhẳng định nào dưới đây đúng?A. $a{<}0, b{<}0, c{>}0, d{<}0$.B. $a{<}0, b{<}0, c{<}0, d{<}0$.C. $a{<}0, b{>}0, c{>}0, d{>}0$.D. $a{<}0, b{>}0, c{<}0, d{<}0$.Lời giải: Từ bảng biến thiên ta thấyHàm số nghịch biến trên khoảng … [Đọc thêm...] vềCho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có bảng biến thiên như sau

Khẳng định nào dưới đây đúng?
Hàm số nào dưới đây có bảng biến thiên như sau?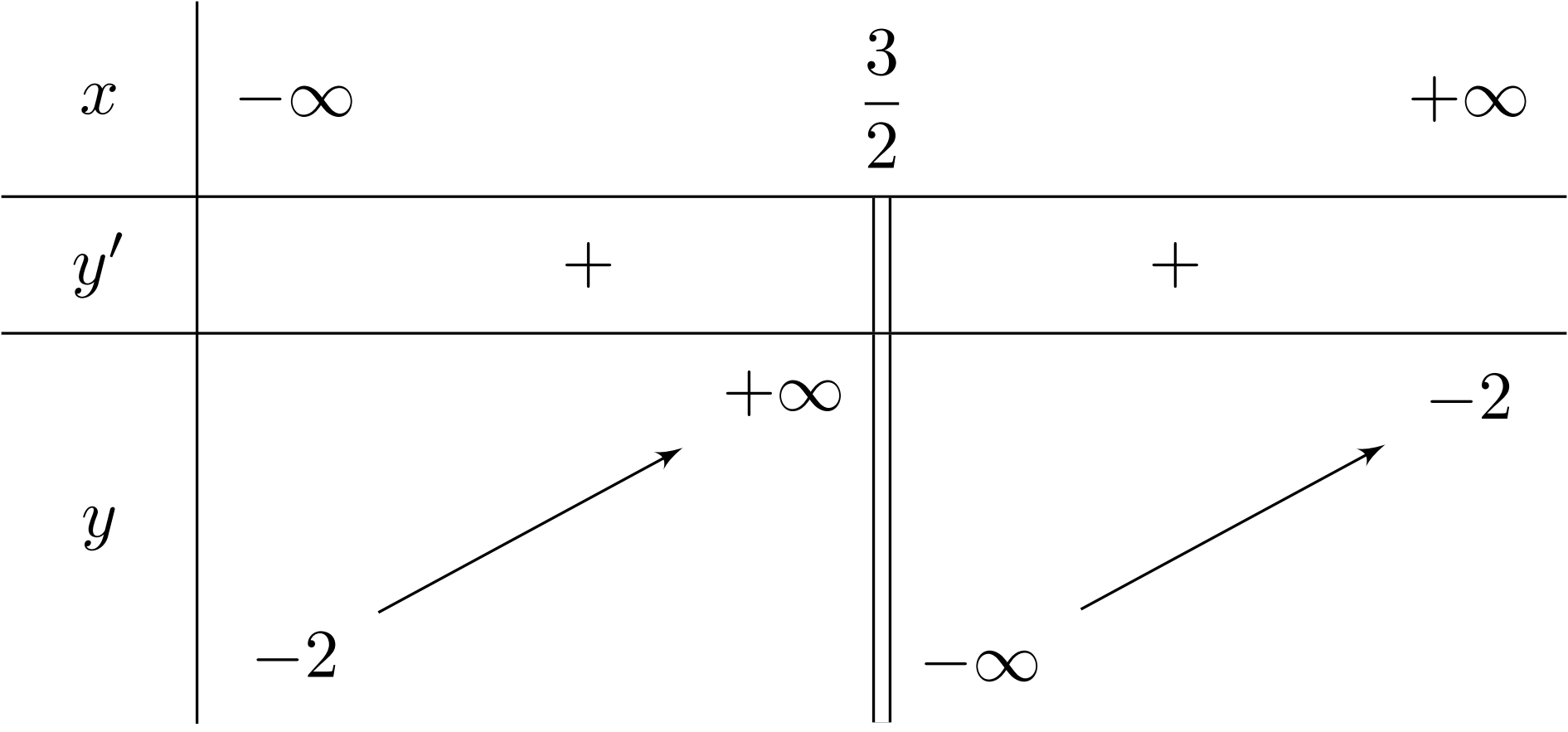

Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y = \dfrac{-4x-3}{2x-1}$.B. $y = \dfrac{2x-3}{-4x-1}$.C. $y = \dfrac{2x-1}{-4x-3}$.D. $y = \dfrac{-4x-1}{2x-3}$.Lời giải: Dựa vào bảng biến thiên ta có$\bullet$ Đạo hàm $y^{\prime} {>} 0 \forall x \neq \dfrac{3}{2}$;$\bullet$ Đồ thị hàm số có tiệm cận đứng là $x = \dfrac{3}{2}$;$\bullet$ Đồ thị hàm … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?

Cho hàm số $y=x^3-3x^2+3x-2$. Điểm nào thuộc đồ thị hàm số?
Bài toán gốc Cho hàm số $y=x^3-3x^2+3x-2$. Điểm nào thuộc đồ thị hàm số?A. $M\left(2;-1\right)$.B. $M\left(1;-3\right)$.C. $M\left(5;61\right)$.D. $M\left(3;7\right)$. Phân tích và Phương pháp giải Dạng toán này yêu cầu nhận biết điểm thuộc đồ thị của hàm số cho trước. Phương pháp giải là thay tọa độ $(x_0; y_0)$ của từng điểm được đề xuất vào … [Đọc thêm...] vềCho hàm số $y=x^3-3x^2+3x-2$. Điểm nào thuộc đồ thị hàm số?
