Trắc nghiệm Đồ thị Hàm số

Bài toán gốc Tìm số giao điểm của đồ thị $(C):y=\dfrac{3x-3}{x+1}$ và $d:y=-x-2$.A. 3.B. 1.C. 2.D. 0.Lời giải: $x^2+6x-1=0$ Phân tích và Phương pháp giải Dạng toán tìm số giao điểm của đồ thị hàm số phân thức bậc nhất trên bậc nhất $y=\dfrac{ax+b}{cx+d}$ và đường thẳng $y=mx+n$. Phương pháp là lập phương trình hoành độ giao điểm, quy đồng và đưa … [Đọc thêm...] vềTìm số giao điểm của đồ thị $(C):y=\dfrac{3x-3}{x+1}$ và $d:y=-x-2$

Bài toán gốc Tìm số giao điểm của đồ thị $(C):y=-x^3-x^2+19x+42$ và $d:y=-2x-3$.A. 1.B. 2.C. 3.D. 0. Phân tích và Phương pháp giải Dạng toán: Tìm số giao điểm của đồ thị hàm số đa thức bậc ba $y=f(x)$ và đường thẳng $y=g(x)$. Phương pháp giải: Lập phương trình hoành độ giao điểm $f(x) = g(x)$. Số nghiệm thực phân biệt của phương trình này chính … [Đọc thêm...] vềTìm số giao điểm của đồ thị $(C):y=-x^3-x^2+19x+42$ và $d:y=-2x-3$.

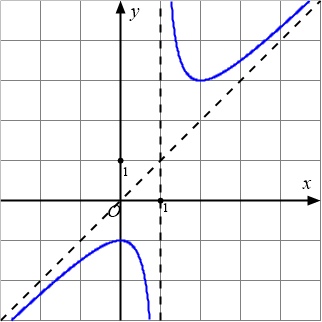
Bài toán gốc Đồ thị dưới đây là của hàm số nào?A. $y=-x^3-x^2-x-1$.B. $y=\dfrac{x-1}{x-1}$.C. $y=x^2-4x+4$.D. $y=\dfrac{x^2-x+1}{x-1}$.Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất. Phân tích và Phương pháp giải Dạng bài toán nhận dạng đồ thị hàm số. Đồ thị gốc có tiệm cận đứng và tiệm cận xiên, đặc trưng cho hàm phân thức bậc hai … [Đọc thêm...] vềĐồ thị dưới đây là của hàm số nào?

Bài toán gốc Cho hàm số $y=f(x)=\dfrac{a_1x^2+b_1x+c_1}{a_2x+b_2}$ có đồ thị như hình dưới đây:Tiệm cận đứng của đồ thị là đường có phương trình $x=m$ tính $m$?A. $2$. Phân tích và Phương pháp giải Đây là dạng bài toán yêu cầu xác định tiệm cận đứng (TCD) của đồ thị hàm số hữu tỉ dựa trên hình vẽ hoặc công thức. Phương pháp giải chung là: Tiệm … [Đọc thêm...] vềCho hàm số $y=f(x)=\dfrac{a_1x^2+b_1x+c_1}{a_2x+b_2}$ có đồ thị như hình dưới đây: