Toán lớp 10

Dạng toán . Ứng dụng bất phương trình và hệ bất phương trình bậc nhất hai ẩn để giải bài toán về kinh tế. Phương pháp giải toán : • Vấn đề tìm miền nghiệm của hệ bất phương trình bậc nhất có liên quan chặt chẽ đến quy hoạch tuyến tính, đó là một ngành toán học có nhiều ứng dụng trong đời sống và kinh tế. • Ta thừa nhận kết quả sau: “Giá trị nhỏ nhất hay lớn nhất của biểu … [Đọc thêm...] vềỨng dụng bất phương trình và hệ bất phương trình bậc nhất hai ẩn để giải bài toán về kinh tế.

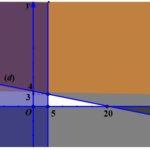
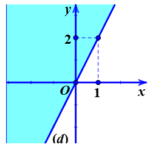
Dạng toán 1. Xác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn. Ví dụ 1 . Xác định miền nghiệm của các bất phương trình sau: a) $2x-y\ge 0.$ b) $\frac{x-2y}{2}>\frac{2x+y+1}{3}.$ a) Trong mặt phẳng tọa độ, vẽ đường thẳng $\left( d \right):\text{ 2}x-y=0$, ta có $\left( d \right)$ chia mặt phẳng thành hai nửa mặt phẳng. Chọn một điểm … [Đọc thêm...] vềXác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Bài tập minh họa Ứng dụng xét dấu của nhị thức bậc nhất vào giải toán Ví dụ 1 . Giải các bất phương trình sau: a) $\left( x-1 \right)\left( 2-3x \right)\ge 0.$ b) $\left( x-2 \right)\left( {{x}^{2}}-5x+4 \right)<0.$ c) $\left( 2x-1 \right)\left( {{x}^{3}}-1 \right)\le 0.$ d) $x\left( \sqrt{3}x-3 \right)\left( 3-{{x}^{2}} \right)\le 0.$ a) Ta có $\left( x-1 … [Đọc thêm...] vềBài tập minh họa Ứng dụng xét dấu của nhị thức bậc nhất vào giải toán

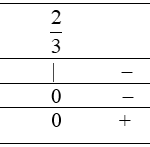
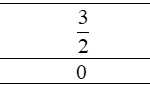
Dạng toán Lập bảng xét dấu biểu thức chứa nhị thức bậc nhất. Ví dụ 1 . Lập bảng xét dấu các biểu thức sau: a) $-2x+3.$ b) $4x-12.$ c) ${{x}^{2}}-4.$ d) $-2{{x}^{2}}+5x-2.$ a) Ta có $-2x+3=0$ $ \Leftrightarrow x=\frac{3}{2}$, $a=-2<0.$ Bảng xét dấu: b) Ta có $4x-12=0$ $\Leftrightarrow x=3$, $a=4>0.$ Bảng xét dấu: c) Ta có: ${{x}^{2}}-4=\left( x-2 … [Đọc thêm...] vềBài tập minh họa Lập bảng xét dấu biểu thức chứa nhị thức bậc nhất

I. Định lí về dấu của nhị thức bậc nhất 1. Nhị thức bậc nhất Nhị thức bậc nhất đổi với x là biểu thức dạng $f(x)=ax+b$trong đó a, b là hai số đã cho, $a \neq 0$ 2. Dấu của nhị thức bậc nhất ĐỊNH LÍ Nhị thức $f(x)=ax+b$có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng $\left ( -\frac{b}{a};+\infty  \right )$,trái dấu với hệ số a khi x lấy … [Đọc thêm...] vềLý thuyết bài Dấu của nhị thức bậc nhất