Bài tập minh họa Ứng dụng xét dấu của nhị thức bậc nhất vào giải toán

Bài tập minh họa Ứng dụng xét dấu của nhị thức bậc nhất vào giải toán

---

Ví dụ 1 . Giải các bất phương trình sau:
a) $\left( x-1 \right)\left( 2-3x \right)\ge 0.$
b) $\left( x-2 \right)\left( {{x}^{2}}-5x+4 \right)<0.$
c) $\left( 2x-1 \right)\left( {{x}^{3}}-1 \right)\le 0.$
d) $x\left( \sqrt{3}x-3 \right)\left( 3-{{x}^{2}} \right)\le 0.$

a) Ta có $\left( x-1 \right)\left( 2-3x \right)=0$ $\Leftrightarrow \left[ \begin{matrix}
x=1 \\
x=\frac{2}{3} \\
\end{matrix} \right.$
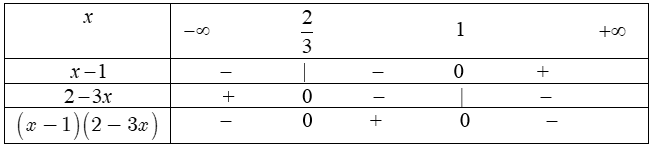
Bảng xét dấu:

Suy ra bất phương trình có tập nghiệm là $S=\left[ \frac{2}{3};1 \right].$
b) Ta có $\left( x-2 \right)\left( {{x}^{2}}-5x+4 \right)$ $=\left( x-2 \right)\left( x-1 \right)\left( x-4 \right).$
Bảng xét dấu:

Suy ra bất phương trình có tập nghiệm là $S=\left( -\infty ;1 \right)\cup \left( 2;4 \right).$
c) Ta có $\left( 2x-1 \right)\left( {{x}^{3}}-1 \right)\le 0$ $\Leftrightarrow \left( 2x-1 \right)\left( x-1 \right)\left( {{x}^{2}}+x+1 \right)\le 0$ $\Leftrightarrow \left( 2x-1 \right)\left( x-1 \right)\le 0$ (vì ${{x}^{2}}+x+1={{\left( x+\frac{1}{2} \right)}^{2}}+\frac{3}{4}>0$).
Bảng xét dấu:

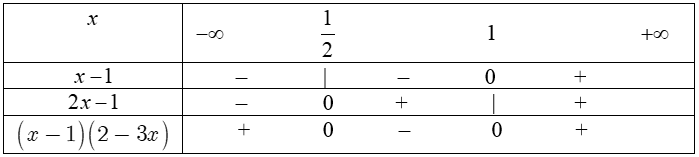
Suy ra bất phương trình có tập nghiệm là $S=\left[ \frac{1}{2};1 \right].$
d) Ta có $x\left( \sqrt{3}x-3 \right)\left( 3-{{x}^{2}} \right)\le 0$ $\Leftrightarrow x\sqrt{3}\left( x-\sqrt{3} \right)\left( \sqrt{3}-x \right)\left( \sqrt{3}+x \right)\le 0$ $\Leftrightarrow -\sqrt{3}x{{\left( x-\sqrt{3} \right)}^{2}}\left( x+\sqrt{3} \right)\le 0$ $\Leftrightarrow \left[ \begin{matrix}
x=\sqrt{3} \\
x\left( x+\sqrt{3} \right)\ge 0 \\
\end{matrix} \right.$
Bảng xét dấu:

Suy ra $x\left( x+\sqrt{3} \right)\ge 0$ $\Leftrightarrow x\in (-\infty ;-\sqrt{3}]\cup [0;+\infty ).$
Vậy tập nghiệm của bất phương trình là: $S=(-\infty ;-\sqrt{3}]\cup [0;+\infty ).$

Ví dụ 2 . Giải các bất phương trình sau:
a) $\frac{-2x+4}{\left( 2x-1 \right)\left( 3x+1 \right)}\le 0.$
b) $\frac{\left( x-3 \right)\left( x+2 \right)}{{{x}^{2}}-1}<1.$
c) $\frac{1}{{{\left( x-2 \right)}^{2}}}\le \frac{1}{x+4}.$

a) Bảng xét dấu:

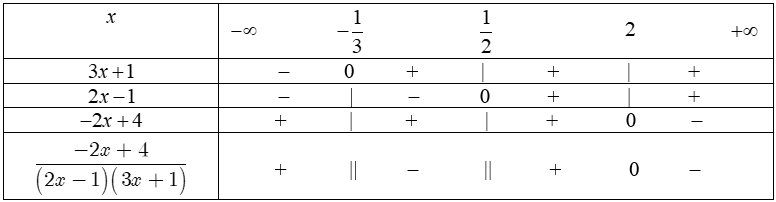
Vậy tập nghiệm của bất phương trình là $S=(-\frac{1}{3};\frac{1}{2})\cup [\text{ 2};+\infty ).$
b) Ta có $\frac{\left( x-3 \right)\left( x+2 \right)}{{{x}^{2}}-1}<1$ $\Leftrightarrow 1-\frac{\left( x-3 \right)\left( x+2 \right)}{{{x}^{2}}-1}>0$ $\Leftrightarrow \frac{x+5}{\left( x-1 \right)\left( x+1 \right)}>0.$
Bảng xét dấu:

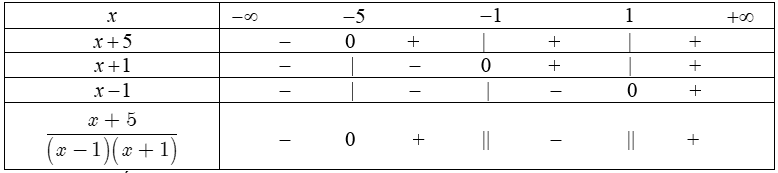
Vậy tập nghiệm của bất phương trình là $S=(-5;-1)\cup (1;+\infty ).$
c) Điều kiện xác định: $\left\{ \begin{matrix}
x\ne 2 \\
x\ne -4 \\
\end{matrix} \right.$
Ta có $\frac{1}{{{\left( x-2 \right)}^{2}}}\le \frac{1}{x+4}$ $\Leftrightarrow \frac{1}{x+4}-\frac{1}{{{\left( x-2 \right)}^{2}}}\ge 0$ $\Leftrightarrow \frac{{{x}^{2}}-4x}{\left( x+4 \right){{\left( x-2 \right)}^{2}}}\ge 0$ $\Leftrightarrow \frac{x\left( x-4 \right)}{\left( x+4 \right){{\left( x-2 \right)}^{2}}}\ge 0$ $\Leftrightarrow \frac{x\left( x-4 \right)}{\left( x+4 \right)}\ge 0.$
Bảng xét dấu:

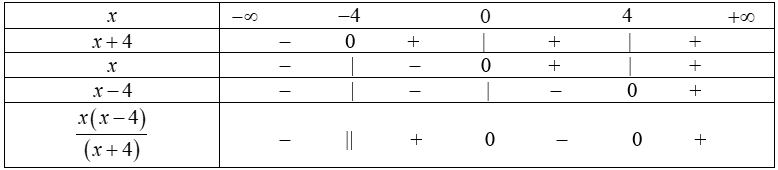
Kết hợp với điều kiện xác định suy ra tập nghiệm của bất phương trình là $S=(-4;0]\cup [4;+\infty ).$

Ví dụ 3 . Giải các bất phương trình sau:
a) $\left| 2x+1 \right|<3x.$
b) $\left| \left| 2x-1 \right|-4 \right|>3.$
c) $\left| x+1 \right|-\left| x-2 \right|\ge 3.$

a)
+ Với $x\ge -\frac{1}{2}$ ta có bất phương trình tương đương với $2x+1<3x$ $\Leftrightarrow x>1.$ Kết hợp với điều kiện $x\ge -\frac{1}{2}$ suy ra bất phương trình có tập nghiệm là $\left( 1;+\infty \right).$
+ Với $x<-\frac{1}{2}$ ta có bất phương trình tương đương với $-2x-1<3x$ $\Leftrightarrow x>-\frac{1}{5}.$ Kết hợp với điều kiện $x<-\frac{1}{2}$ suy ra bất phương trình vô nghiệm.
Vậy tập nghiệm của bất phương trình là $S=\left( 1;+\infty \right).$
b) Ta có $\left| \left| 2x-1 \right|-4 \right|>3$ $\Leftrightarrow \left[ \begin{matrix}
\left| 2x-1 \right|-4>3 \\
\left| 2x-1 \right|-4<-3 \\
\end{matrix} \right.$ $\Leftrightarrow \left[ \begin{matrix}
\left| 2x-1 \right|>7 \\
\left| 2x-1 \right|<1 \\
\end{matrix} \right.$ $\Leftrightarrow \left[ \begin{matrix}
\begin{align}
& 2x-1>7 \\
& 2x-1<-7 \\
\end{align} \\
-1<2x-1<1 \\
\end{matrix} \right.$ $\Leftrightarrow \left[ \begin{matrix}
\begin{align}
& x>4 \\
& x<-3 \\
\end{align} \\
0<x<1 \\
\end{matrix} \right.$
Vậy tập nghiệm của bất phương trình là $S=\left( -\infty ;-3 \right)\cup \left( 0;1 \right)\cup \left( 4;+\infty \right).$
c) Bảng xét dấu:

Từ bảng xét dấu đó ta chia ra các trường hợp sau:
+ Với $x<-1$ ta có bất phương trình tương đương với $-\left( x+1 \right)+\left( x-2 \right)\ge 3$ $\Leftrightarrow -3\ge 3$ (vô nghiệm).
+ Với $-1\le x<2$ ta có bất phương trình tương đương với $\left( x+1 \right)+\left( x-2 \right)\ge 3$ $\Leftrightarrow x\ge 2.$ Kết hợp với điều kiện $-1\le x<2$ suy ra bất phương trình vô nghiệm.
+ Với $x\ge 2$ ta có bất phương trình tương đương với $\left( x+1 \right)-\left( x-2 \right)\ge 3$ $\Leftrightarrow 3\ge 3.$ Kết hợp với điều kiện $x\ge 2$ suy ra bất phương trình có nghiệm là $x\ge 2.$
Vậy tập nghiệm của bất phương trình là $S=[2;+\infty ).$

Ví dụ 4 . Giải các bất phương trình sau:
a) $\frac{\left| x-2 \right|-x}{x}<1.$
b) $\frac{\left| x-1 \right|-1}{{{x}^{4}}-{{x}^{2}}}\ge 0.$

a)
+ Với $x\ge 2$ ta có bất phương trình tương đương với $\frac{x-2-x}{x}<1$ $\Leftrightarrow \frac{-2}{x}<1$ $\Leftrightarrow x>-2.$ Kết hợp điều kiện $x\ge 2$ suy ra tập nghiệm bất phương trình là ${{S}_{1}}=[2;+\infty ).$
+ Với $x<2$ ta có bất phương trình tương đương với $\frac{2-x-x}{x}<1$ $\Leftrightarrow \frac{2-2x}{x}<1$ $\Leftrightarrow 1-\frac{2-2x}{x}>0$ $\Leftrightarrow \frac{3x-2}{x}>0.$
Bảng xét dấu:

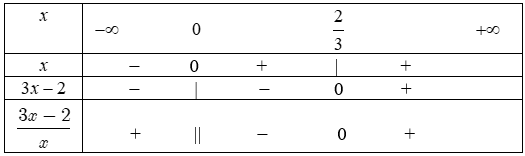
Kết hợp điều kiện $x<2$ suy ra tập nghiệm bất phương trình là ${{S}_{2}}=(-\infty ;0)\cup (\frac{2}{3};2).$
Vậy tập nghiệm bất phương trình là $\text{S}={{S}_{1}}\cup {{S}_{2}}=(-\infty ;0)\cup (\frac{2}{3};+\infty ).$
b) Điều kiện xác định: ${{x}^{4}}-{{x}^{2}}\ne 0$ $\Leftrightarrow \left\{ \begin{matrix}
x\ne 0 \\
x\ne \pm 1 \\
\end{matrix} \right.$
Ta có $\frac{\left| x-1 \right|-1}{{{x}^{4}}-{{x}^{2}}}\ge 0$ $\Leftrightarrow \frac{\left( \left| x-1 \right|+1 \right)\left( \left| x-1 \right|-1 \right)}{{{x}^{4}}-{{x}^{2}}}\ge 0$ $\Leftrightarrow \frac{{{\left| x-1 \right|}^{2}}-1}{{{x}^{4}}-{{x}^{2}}}\ge 0$ $ \Leftrightarrow \frac{{{x^2} – 2x}}{{{x^4} – {x^2}}} \ge 0$ $ \Leftrightarrow \frac{{x\left( {x – 2} \right)}}{{{x^2}\left( {x – 1} \right)\left( {x + 1} \right)}} \ge 0$ $ \Leftrightarrow \frac{{x – 2}}{{x\left( {x – 1} \right)\left( {x + 1} \right)}} \ge 0.$
Bảng xét dấu:

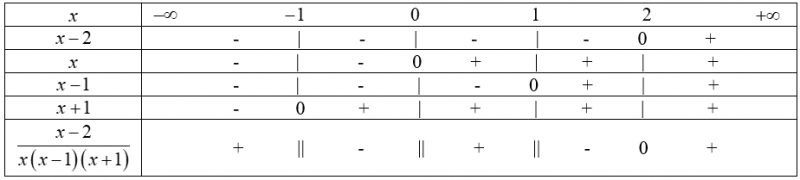
Vậy tập nghiệm bất phương trình là: $S = \left( { – \infty ; – 1} \right) \cup \left( {0;1} \right) \cup \left[ {2; + \infty } \right).$